Współczynnik przenikania ciepła stolarki okiennej o zmiennej konfiguracji

Ocena ta jest niezwykle ważna szczególnie teraz, kiedy konsumenci stolarki okiennej decydują się na okna o dużych, często niestandardowych rozmiarach i kształtach, które mają pełnić funkcję przeszklonych ścian.

Konieczność takiej oceny powstaje również z faktu, że okno składa się z kilku elementów ze zróżnicowanymi wartościami parametrów cieplnych. Jednak zarówno w literaturze naukowo-technicznej, jak i w materiałach marketingowych producentów stolarki okiennej ciężko jest znaleźć charakterystyki cieplne dla całego okna.

Pojawiły się ostatnio artykuły z wynikami badań wpływu wybranych czynników na współczynnik przenikania ciepła stolarki okiennej w budynkach mieszkalnych [1, 2], w których przeanalizowano współczynnik U_w stolarki okiennej w zależności od wybranych czynników dla okien jedno- i wieloskrzydłowych. Jednak te badania dotyczyły okien, których rozmiary były bliskie rozmiarom okna standardowego. Przy czym analizie poddano okna o stałej wysokości, tj. 1,48 m, co w żaden sposób nie może zadawalać architektów.

Również można oczekiwać pretensji od kolegów architektów w związku z przyjętą w tych badaniach prawie jednakową konfiguracją okien, tj. stałą proporcją ich wysokości i szerokości.

Można zgodzić się z tym, że na danym etapie rozwoju techniki budowlanej mamy charakterystyki cieplne produkowanych elementów okien na jakimś określonym poziomie i niecodziennie te charakterystyki się zmieniają. Jednak co dotyczy czynników geometrycznych, to ich wybór i wpływ przy projektowaniu praktycznym tworzą codziennie pytania u projektantów. Łatwo można zrozumieć architektów, że istnieje konieczność uzyskania wiedzy na ten temat.

W związku z powyższym, celem danego badania jest analiza współczynnika przenikania ciepła stolarki okiennej, wykonanej z PCV, w zależności od grupy czynników w najwyższym stopniu i bezpośrednio charakteryzujących konfigurację okien:

• pola powierzchni okna,
• proporcji okna, wyrażonej stosunkiem wysokości do szerokości,
• liczby skrzydeł okiennych i szerokości elementów ramy, wraz z oceną stopnia i charakteru wpływu tych czynników

oraz określeniem ich wartości optymalnych na podstawie deterministycznego modelu matematycznego opracowanego z danych eksperymentu obliczeniowego.

Metoda obliczania współczynnika przenikania ciepła stolarki okiennej o zmiennej konfiguracji

Przegrody budowlane, między innymi jak również okna w ścianach budynków, składają się z kilku różnych materiałów połączonych ze sobą w różny sposób.

Do obliczenia współczynnika przenikania ciepła przegród składających się z elementów oszklonych i/lub nieprzezroczystych, włożonych w ramy lub połączonych z nimi wykorzystuje się dwie metody [3] - zbiorczą i składnikową. Nie uwzględniają one efektów promieniowania, przenoszenia ciepła spowodowanego wypływaniem powietrza, efektu żaluzji itp. Jednak po przeanalizowaniu możliwości tych metod autorzy przekonali się co do ich przydatności do realizacji celów danego badania.

Przy czym uznano, że do obliczania współczynnika przenikania ciepła stolarki okiennej o zmiennej konfiguracji najbardziej przydatna i oczywista jest składnikowa metoda oceny. Metoda ta dzieli fragment przegrody na pola powierzchni o różnych właściwościach cieplnych, a całkowity współczynnik przenikania ciepła oblicza się za pomocą ważonych powierzchniowo wartości U elementów składowych z dodatkowymi członami korekcyjnymi, uwzględniającymi wzajemne oddziaływania cieplne między tymi elementami [3]. Według tej metody współczynnik przenikania ciepła U_w pojedynczego okna należy obliczać zgodnie z równaniem:

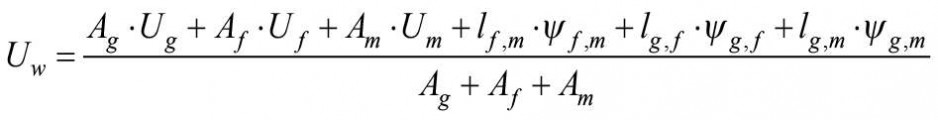(1)

gdzie:

U_g, U_ƒ, U_m - współczynniki przenikania ciepła, odpowiednio:
   - oszklenia,
   - ramy,
   - słupków okiennych,
Ψ_ƒ,m, Ψ_g,ƒ, Ψ_g,m - liniowe współczynniki przenikania ciepła spowodowane połączonymi efektami cieplnymi elementów, odpowiednio:
   - szklącego i ramy,
   - szklącego i słupka,
   - ramy i słupka okiennego,
l_g,f , l_g,m , l_f,m - długość liniowego mostku cieplnego powstającego na styku, odpowiednio:
   - szkła i ramy,
   - szkła i słupka,
   - ramy i słupka,
A_g, A_m, A_f - pole powierzchni, odpowiednio:
   - oszklenia,
   - słupków okiennych,
   - ramy.

Odnosząc się do przedstawionego wzoru, autorzy stworzyli algorytm do wyliczania szukanego współczynnika przenikania ciepła okna U_w przy zmianie wartości wybranych czynników, który stanowił podstawę do opracowania modelu matematycznego.

Badane warianty okien o zmiennej konfiguracji oraz model matematyczny do określenia ich współczynnika przenikania ciepła

Rozmiary współczesnych okien w budynkach mieszkalnych ograniczone są gabarytami pomieszczeń. Wysokość okien może osiągać 2,5 m. Szerokość okien waha się w dużym zakresie, nawet od 0,60 do 3-4 m. W oknach stosuje się poziome rygle. Jednak częściej mogą występować pionowe słupki, tworząc w oknie kilka skrzydeł.

Z uwzględnieniem najczęściej stosowanych rozmiarów okien oraz postawionego celu badania zostały wybrane następujące warianty stolarki okiennej:

• powierzchnia od 1,82 m² (okno standardowe) do 5,46 m²;
• stosunek wysokości okna do jego szerokości - od 0,5 do 1;
• liczba skrzydeł - do 1 do 3.

Schematy badanych wariantów okien podano na RYS. 1-3.

Przy opracowaniu modelu matematycznego bardzo ważne jest, by zapewnić jego praktyczną przydatność oraz skuteczność. Takie cechy można osiągnąć, opracowując krótkie modele, w których wykorzystano najważniejsze czynniki, opisujące badany proces czy właściwości oraz zapewniające uzyskanie informacji interesującej odbiorców stolarki okiennej. Przy tym czynniki w modelu należy przyjmować jako sterowalne, jednoznaczne, niesprzeczne i wzajemnie niezależne [4].

Z uwzględnieniem przyjętego celu badania jako funkcję celu Y wybrano współczynnik przenikania ciepła wieloskrzydłowej stolarki okiennej U_w [W/(m2·K)].

Badano zależność współczynnika U_w od następujących czynników:

• pola powierzchni okna A₀(czynnik X₁),
• proporcji okna θ, wyrażonej stosunkiem wysokości okna do jego szerokości (czynnik X₂),
• liczby skrzydeł okiennych r (czynnik X₃),
• szerokości elementów ramy b_f (czynnik X₄).

Przypuszczano, że szukaną zależność Y = ƒ (X₁, X₂, X₃, X₄) może opisywać wielomian drugiego stopnia.

Do uzyskania danych dla opisu tej zależności przeprowadzono 4-czynnikowy eksperyment obliczeniowy według planu drugiego stopnia. Zastosowano kompozycyjny symetryczny trójpoziomowy D-optymalny plan, zawierający 24 próby [4].

Do wyliczenia wartości Y_i w 24 wierszach planu wykorzystano oprogramowanie Microsoft Excel.

Na RYS. 4 został przedstawiony schemat blokowy wyliczania współczynnika przenikania ciepła okien o zmiennej konfiguracji. Zaproponowany algorytm obliczeń wykorzystano do realizacji eksperymentu obliczeniowego, z którego wyniki zastosowano do opracowania deterministycznego modelu matematycznego współczynnika przenikania ciepła stolarki okiennej.

Przed rozpoczęciem obliczeń wykonano uzasadniony wybór zakresu zmienności czynników oraz wartości zmiennych stałych, od których także zależą efekty wpływu rozpatrywanych czynników. Wybierając zakres zmienności pola powierzchni okna, proporcji okien itp., opierano się na informacji, uzyskanej z konsultacji z architektami i producentami stolarki okiennej.

• Pole powierzchni okna A₀ (czynnik X₁) na dolnym poziomie przyjęto równe 1,82 m², tj. odpowiednie polu powierzchni okna referencyjnego [5].
• Jako górny poziom przyjęto powierzchnię okna trzykrotnie zwiększoną - 5,46 m².
• Odpowiednio na średnim poziomie przyjęto 3,64 m², czyli dwukrotnie większe okno niż okno standardowe.
• Proporcje okien, wyrażone stosunkiem wysokości do szerokości okna θ (czynnik X₂), przyjęto na poziomach 0,5, 0,75 i 1,0.

Pozwala to rozpatrywać okna w dużym zakresie zmiany ich zarysu zewnętrznego - od prostokąta z proporcją 1:2 do kwadratu z proporcją 1:1.

Liczba skrzydeł okiennych r (czynnik X₃) mogła być wybrana dowolnie. Jednakże dla budynków mieszkalnych z uwzględnieniem najczęściej stosowanych typów okien miało sens ograniczyć się do 3 skrzydeł. Tak więc wybrano:

• 1 skrzydło jako poziom dolny,
• 2 skrzydła jako poziom średni,
• 3 skrzydła jako poziom górny.

Szerokość elementów ramy b_ƒ (czynnik X4) przyjęto z uwzględnieniem współczesnych materiałów oraz technologii wytwarzania i montażu stolarki okiennej. Wybrano trzy poziomy tego czynnika: dolny - 0,08, średni - 0,12, górny - 0,16 m.

Pozostałe wielkości geometryczne wymienione we wzorze (1) wyliczano na podstawie wartości wybranych czynników.

Wartości współczynników przenikania ciepła oszklenia U_g i ramy U_ƒ przyjęto według danych producentów stolarki okiennej:

• U_g = 1,0 W/(m²·K) (pakiet szklący ze standardowym oszkleniem dwuszybowym),
• U_ƒ = 1,3 W/(m²·K) (rama grubości zabudowy 70 mm ze standardowym wzmocnieniem stalowym).

Wartość U_m dla słupków okiennych została przyjęta na tym samym poziomie, co wartość współczynnika przenikania ciepła ramy U_ƒ. Wartości ψ_ƒ,m, ψ_g,ƒ, ψ_g,m przyjęto równe 0,080 W/(m·K) [6].

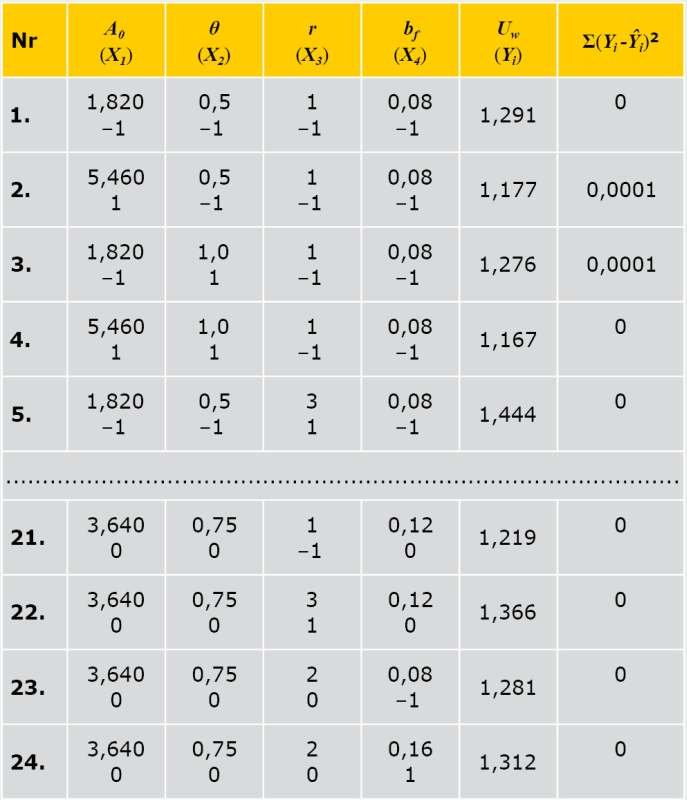
Wyżej wymienione wartości naturalne czynników Ẋ₁, Ẋ₂, Ẋ₃, Ẋ₄ i odpowiadające im wartości unormowane X₁, X₂, X₃, X₄ przedstawiono w TABELI.

Przejście z wartości naturalnych Ẋ_i do unormowanych X_i wyraża się wzorem:

X_i = [2Ẋ_i –(Ẋ_imax +Ẋ_imin)]/(Ẋ_imax – Ẋ_imin)    (2)

gdzie:

Ẋ_i, Ẋ_imax, Ẋ_imin - odpowiednio bieżące, maksymalne i minimalne wartości naturalne i-tego czynnika.

Na podstawie wyników obliczeń (TABELA) metodą najmniejszych kwadratów [7] opracowano równanie regresji zależności Y = ƒ(X₁, X₂, X₃, X₄). Istotność współczynników tego równania oceniono za pomocą t-kryterium.

Metoda testowania współczynników szczegółowo opisana została przez autorów w [1]. W wyniku testu 6 współczynników okazało się nieistotnych.

Po ich usunięciu przyjęto postać końcową równania z k + 1 = 9 współczynnikami:

Ŷ = 1,298 – 0,065X₁ + 0,006X₂ + 0,072X₃ + 0,010X₄ – 0,008X1X₃ + 0,006X1X₄ + 0,011X2X₃ – 0,006X₃X₄ + 0,022X₁  (3)

Potwierdzona została również adekwatność uzyskanego modelu według metody opisanej w [8].

Dany model posiadał:

• Σ(Y_i – Ŷ_i)² = 0,0008;
• S²_a = Σ(Y_i -Ŷ_i)²/(N – (k+1)) = 0,0001;
• R² = 0,9952.

Dodatkowo jakość aproksymacji danych opracowanym równaniem oceniono według kryterium F [8].

Przy poziomie istotności α = 0,05 i liczbie stopni swobody ƒ₁ = N – 1 = 24 – 1 = 23, ƒ₂ = N – (k + 1) = 24 – 15 = 9 okazało się, że wartość obliczeniowa kryterium F₀ = S²_y /S²_a = 82,2085 wielokrotnie przekracza wartość tabelaryczną F_0,05;23;9 = 2,9235 [8], co potwierdza wysoką jakość modelu.

Analiza wpływu wybranych czynników na współczynnik przenikania ciepła okien o zmiennej konfiguracji

Za pomocą równania regresji (3) przeanalizowano stopień i charakter wpływu poszczególnych czynników na współczynnik przenikania ciepła U_w okna. Analizę przeprowadzono dla zmiennych w postaci naturalnej. Interesowały nas przede wszystkim warianty stolarki okiennej o najniższym współczynniku U_w.

Wykryto, że na współczynnik U_w korzystny wpływ okazuje tylko jeden czynnik - powierzchnia okna A₀(X₁). Przy zmianie A₀ od 1,82 do 5,46 m2 wartość współczynnika U_w zmalała o 9,4%. Ze wzrostem pozostałych czynników θ (X₂), r (X₃), b_f (X₄) współczynnik U_w rośnie.

Przy zmianie wartości tych czynników z dolnego (–1) do górnego (+1) poziomu ich niekorzystne wkłady w podwyższenie U_w wynoszą:

• proporcji okna θ (X₂)o 1,0%,
• liczby skrzydeł r(X₃) o 11,7%,
• szerokości elementów ramy b_f (X₄) o 1,6%.

Jak widać, istotny wkład wykazał tylko czynnik r(X₃) - liczba skrzydeł. Przy czym wykryto, że dla rozpatrywanych warunków na każde dodane skrzydło, przy przyjętym średnim poziomie pozostałych zmiennych, współczynnik U_w okna rośnie równomiernie o około 6%.

Mimo oczekiwań, w przyjętym zakresie zmienności czynniki θ (X₂) oraz b_ƒ (X₄) nie wykazały istotnego wpływu na wartość współczynnika U_w. Czynnik θ (X₂) nie okazuje bezpośredniego oddziaływania na współczynnik U_w, lecz poprzez długość mostku liniowego na styku szkło-rama.

Z obliczeń wynika, że długość tego mostka przy zmianie kształtu okna od kwadratu z proporcjami 1:1 do prostokąta 1:2 wzrasta o około 6%. Jednak kilkunastokrotnie mniejsza wartość liniowego współczynnika przenikania ciepła mostka w porównaniu z wartościami współczynników przenikania ciepła szkła i ramy ostatecznie osłabia do 1% wkład czynnika θ (X₂) (poprzez iloczyn L_g,f i y_g,ƒ) w podwyższenie współczynnika U_w.

Czynnik b_ƒ(X₄) okazuje wpływ na współczynnik U_w też nie w bezpośredni sposób, lecz poprzez powierzchnię ramy.

Z obliczeń wynika, że zmiana szerokości elementów ramy b_ƒ z 0,08 do 0,16 m przy przyjętym średnim poziomie pozostałych zmiennych, zwiększa powierzchnię ramy Ag o około 82,6%. W takim razie można byłoby oczekiwać istotnego wpływu czynnika b_ƒ (X₄) na współczynnik U_w.

Jednak nie wykryto takiego wpływu, ponieważ powierzchnie okna A₀, szkła A_g i ramy A_f powiązane są warunkiem:

A₀ = A_g + A_f   (4)

Oznacza to, że przy stałej wartości A₀ ze wzrostem A_f, spowodowanym zwiększeniem b_ƒ, równo w takim samym stopniu zmaleje powierzchnia szkła A_g. Wtedy ich wkłady w podwyższenie współczynnika U_w poprzez iloczyny A_gU_g i A_ƒU_ƒ będą zależały od różnicy pomiędzy U_g a U_ƒ.

 W związku z niewielkim zróżnicowaniem pomiędzy tymi zmiennymi [w naszym badaniu U_g= 1,0, U_ƒ = 1,3 W/(m2·K)], wkłady od zmian powierzchni A_gU_g i A_ƒU_ƒ wzajemnie się neutralizują, a ich sumaryczny efekt odzwierciedlający wpływ czynnika b_ƒ (X₄) wyniósł jedynie 1,6%.

Tak więc możemy stwierdzić, że w praktyce projektowania, przy wyborze konfiguracji okien i oszacowaniu ich właściwości cieplnych, takie czynniki jak proporcja okna θ oraz szerokość elementów ramy b_ƒ należy uważać za nieistotne i one mogą być pomijane.

Odnośnie czynnika r(X₃) - liczby skrzydeł, można stwierdzić, że nieznacznie wzmacnia on korzystny efekt czynnika A₀(X₁). Przy zmianie r od 1 do 3 wkład wahań czynnika A₀ w obniżenie współczynnika U_w wzrasta i wynosi 8,7% (r = 1) i 10,0% (r = 3).

Opisany charakter wpływu czynników odzwierciedlają wykresy na RYS. 5, na którym pokazano graficzną zależność U_w = ƒ (A₀) dla r = 1, r = 2 oraz r = 3.

W wyniku optymalizacji równania regresji (3) wykryto, że uzyskana funkcja osiąga minimalną (najlepszą) wartość U_w,min= 1,164 W/(m2·K) przy następujących wartościach czynników: 

• A0(X1) = 5,46 m2,
• θ (X2) = 1,
• r(X3) = 1,
• bƒ (X4) = 0,08 m.

Natomiast maksymalną (najgorszą) wartość U_w,max = 1,484 W/(m2·K) obserwuje się przy:

• A0(X1) = 1,82 m2,
• θ (X2) = 1,
• r(X3) = 3,
• bƒ (X4) = 0,08 m.

Zaproponowany model matematyczny dla zbioru dowolnych wartości badanych czynników (z przyjętych w tym badaniu zakresów zmienności) po ich unormowaniu według wzoru (2) pozwala obliczyć współczynnik przenikania ciepła stolarki okiennej w dowolnej z wybranych do badania konfiguracji (RYS. 1-3).

Model również może być wykorzystany do numerycznego sterowania obiektem badania.

Wnioski

Opracowany deterministyczny model matematyczny pozwolił dokładnie określić charakter i stopień wpływu podstawowych czynników geometrycznych na współczynnik przenikania ciepła U_w stolarki okiennej o zmiennej konfiguracji. Wykryto, że na współczynnik U_w korzystny wpływ okazuje jedynie powierzchnia okna A₀.

Przy zmianie A₀ od 1,82 do 5,46 m2 wartość współczynnika U_w zmalała o 9,4%. Na odwrót zaś, przy wzroście liczby skrzydeł r od 1 do 3, współczynnik U_w wzrasta o 11,7%.

Czynniki θ - proporcje okna oraz b_ƒ - szerokość elementów ramy nie wykazały istotnego wpływu na wartość współczynnika U_w i w praktyce projektowania przy wyborze konfiguracji okien i oszacowaniu ich właściwości cieplnych mogą być pomijane.

Ustalono, że optymalne wartości zbadanych parametrów dla stolarki okiennej zbadanych konfiguracje to są: 

• A0 = 5,46 m2,
• θ = 1,
• r = 1,
• bƒ = 0,08 m.

Pozwalają one osiągnąć minimalną wartość współczynnika U_w,min = 1,164 W/(m2·K).

Zaproponowany model matematyczny dla zbioru dowolnych wartości badanych czynników (z przyjętych dla nich zakresów zmienności) po ich unormowaniu pozwala obliczyć współczynnik przenikania ciepła stolarki okiennej dowolnej z wybranych konfiguracji.

Literatura

1. W. Jezierski, J. Borowska, "Analiza parametrów cieplnych współczesnej stolarki okiennej", "IZOLACJE" 4/2017.
2. W. Jezierski, J. Borowska, "Parametry cieplne wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych", "IZOLACJE" 6/2017.
3. PN-EN ISO 12631:2013-03, "Cieplne właściwości użytkowe ścian osłonowych. Obliczanie współczynnika przenikania ciepła".
4. Z. Polański, "Planowanie doświadczeń w technice", PWN, Warszawa 1984.
5. PN-EN 14351-1+A2:2016-10, "Okna i drzwi część 1: Okna i drzwi zewnętrzne bez właściwości dotyczących odporności ogniowej i/lub dymoszczelności".
6. PN-EN ISO 14683:2008, "Mostki cieplne w budynkach. Liniowy współczynnik przenikania ciepła. Metody uproszczone i wartości orientacyjne".
7. K. Hartmann, E. Lezki, W. Schär, "Statistische Versuchsplanung und - auswertung in der Stoffwirtschaft", VEB, Leipzig 1977.
8. W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska, M. Wasilewski, "Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach. Część II. Statystyka matematyczna", PWN, Warszawa 2003.

Chcesz być na bieżąco? Zapisz się do naszego newslettera!