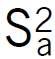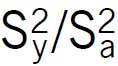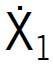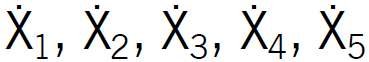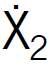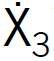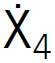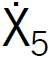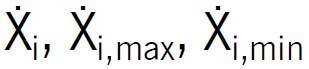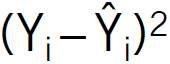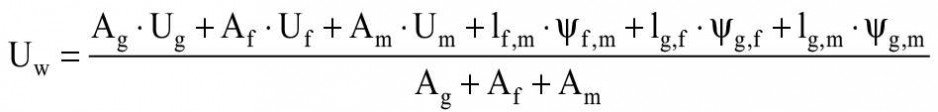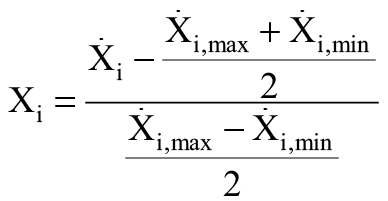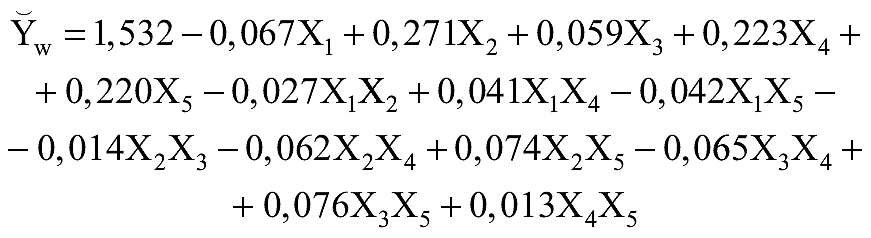Parametry cieplne wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych
Thermal performance of multi-wing window joinery in residential buildings

Jak zmienia się wartość współczynnika przenikania ciepła wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych w zależności od powierzchni okna, liczby skrzydeł w oknie, szerokości elementów ramy itp.?
www.pixabay.com
Okna o większej ilości skrzydeł charakteryzują się zwykle wyższą, mniej korzystną, wartością współczynnika przenikania ciepła niż okna jednoskrzydłowe. Wiąże się to przede wszystkim ze zwiększeniem powierzchni ramy okiennej i długości mostka termicznego na styku szkło–rama oraz zmniejszeniem powierzchni szklonej okna. Ostatecznie potwierdzić tę tezę można jednak poprzez prawidłowo zaplanowane i realizowane badanie.
Zobacz także
BREVIS S.C. Czy nawiewniki w oknach są obowiązkowe – najważniejsze Informacje

Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu...
Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu uniknięcia negatywnych skutków zbyt dużej wilgotności, to już dyskomfort siedzenia w dusznym i nieprzewietrzonym pomieszczeniu zna każdy. Oprócz wentylacji grawitacyjnej do niedawna odpowiednią cyrkulację powietrza zapewniały nieszczelności w oknach. Jednak rozwój technologiczny i zwiększenie szczelności...
DAKO Jak wybrać drzwi do nowoczesnego domu?

Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie...
Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie aspekty trzeba zwrócić szczególną uwagę, wybierając drzwi zewnętrzne!
RoletyAlu Sp. z o.o. Jak łatwo kupić rolety zewnętrzne przez internet?

Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość...
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość złożenia zamówienia bezpośrednio u producenta rolet zewnętrznych pozwala wyeliminować pośredników, co skraca czas potrzeby na realizację zamówień i przekłada się na dużo niższe ceny.
Zarówno w specjalistycznej literaturze, jak i w materiałach marketingowych producentów stolarki okiennej bardzo trudno doszukać się charakterystyki cieplnej okien wieloskrzydłowych (wielokwaterowych). Zazwyczaj podane są informacje (czasem pojedyncze wyliczenia) dla okna standardowego, czyli okna jednoskrzydłowego o wymiarach 1,23×1,48 m.
W numerze 4/2017 "IZOLACJE" opublikowano artykuł pod tytułem "Analiza parametrów cieplnych współczesnej stolarki okiennej", dotyczący analizy współczynnika przenikania ciepła stolarki okiennej w zależności od czynników geometrycznych i fizyko-technicznych, w którym opracowano czteroczynnikowy model matematyczny dla najprostszego wariantu - stolarki okiennej jednoskrzydłowej [1]. We wspomnianym artykule nie rozpatruje się zmiennej liczby skrzydeł i w związku z tym opracowany model ma ograniczone możliwości do oceny współczynnika Uw okien. W niniejszej pracy zaprezentowano zasady opracowania pięcioczynnikowego modelu matematycznego współczynnika przenikania ciepła stolarki okiennej przy zmiennej liczbie skrzydeł.
ABSTRAKT |
|
W artykule przedstawiono analizę współczynnika przenikania ciepła wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych w zależności od powierzchni okna, liczby skrzydeł w oknie, szerokości elementów ramy, współczynnika przenikania ciepła powierzchni szklonej oraz współczynnika przenikania ciepła ramy. Analiza została wykonana w oparciu o deterministyczny model matematyczny omówionej zależności, opracowany na podstawie wyników z eksperymentu obliczeniowego. Informacja może być przydatna dla studentów, naukowców, projektantów i konsumentów stolarki okiennej. |
Thermal performance of multi-wing window joinery in residential buildingsThe article presents the analysis of heat transfer coefficient values for multi-wing window joinery in residential buildings according to the surface area of the window, the number of wings in the window, the width of the frame components, and the heat transfer coefficient values for glazed surfaces and frames. The analysis was based on a deterministic mathematical model of the relationship concerned, based on the results of a computational experiment. This information can be useful for students, scientists, designers and consumers of window joinery. |
Celem artykułu jest analiza współczynnika przenikania ciepła wieloskrzydłowej stolarki okiennej wykonanej z PCW w zależności od:
- powierzchni okna,
- liczby skrzydeł w oknie,
- szerokości elementów ramy,
- współczynnika przenikania ciepła powierzchni szklonej
- a także współczynnika przenikania ciepła ramy z oceną stopnia i charakteru wpływu tych czynników oraz określeniem ich wartości optymalnych na podstawie opracowanego deterministycznego modelu matematycznego.
Współczesne okna wieloskrzydłowe
Zasadniczym elementem konstrukcyjnym, który odróżnia okna jednoskrzydłowe od wieloskrzydłowych, jest słupek okienny. Można go nazwać swoistą cechą podziału okna. Po otwarciu skrzydeł to właśnie on wskazuje, jak przebiega podział ościeżnicy okiennej (pionowy lub poziomy).
W przypadku okien wielokwaterowych (gdy okno podzielone jest na pola poziome lub pionowe i poziome) charakterystyczne są szprosy bądź szczebliny. Są to elementy poprzeczne zamocowane w ościeżnicy dzielące skrzydła na mniejsze pola.
W stolarce okiennej kilkudzielnej osadzone obok skrzydła mogą być przedzielone słupkiem stałym lub ruchomym. Istnieje także opcja bezsłupkowa, kiedy skrzydło przymyka się jedno na drugie.
W przypadku okien z ramą wykonaną z drewna bez słupka stałego można wyróżnić skrzydła
- przymykane (nachodzą od zewnątrz),
- a także przymykowe (nachodzą dzięki wykorzystaniu specjalistycznego profilu nazywanego listwą przymykową).
Wykorzystywane w oknach wielokwaterowych szprosy można podzielić na dwie zasadnicze grupy: szprosy konstrukcyjne albo imitacje. Pierwsze pełnią rolę podobną do słupków pionowych. Drugie służą zaś do osiągnięcia efektów estetycznych. Montuje się je dwojako albo przykleja się je do tafli szyby, albo wmontowuje się wewnątrz pakietów szybowych.
W literaturze niezwykle trudno jest odnaleźć dane odnośnie współczynnika Uw okna wielokwaterowego.
![TABELA 1. Współczynnik przenikania ciepła okna składającego się z różnej ilości kwater [źródło: strona internetowa: www.cieplej.pl.] TABELA 1. Współczynnik przenikania ciepła okna składającego się z różnej ilości kwater [źródło: strona internetowa: www.cieplej.pl.]](https://www.izolacje.com.pl/media/cache/typical_view/data/202012/b-parametry-cieplne-wieloskrzydlowej-stolarki-tab1.jpg)
TABELA 1. Współczynnik przenikania ciepła okna składającego się z różnej ilości kwater [źródło: strona internetowa: www.cieplej.pl.]
W TAB. 1 zamieszczono informacje z zasobów Dolnośląskiej Agencji Energii i Środowiska [2], w których przedstawione są dane dla okien kwaterowych o wymiarach jedynie 1,80×2,40 m.
- Przedostatni wiersz TAB. 1 mówi o wysokości współczynnika przenikania ciepła dla takiego okna.
- Ostatni wiersz informuje, jakim procentem współczynnika przenikania ciepła okna jednokomorowego jest analizowane okno o odpowiednio zwiększonej liczbie komór.
Przytoczone dane pokazują, że współczynnik U, przy niezmiennych wartościach Ug, Uf i ψ, rośnie wraz ze zwiększającą się liczbą komór:
- dla okna jednokomorowego, przy zadanych warunkach, wynosi 1,1 W/(m2·K),
- natomiast dla okna ośmiokomorowego o takich samych wymiarach wzrasta już do 1,38 W/(m2·K), czyli wynosi aż o 25% więcej [2].
Dane te mają jednak charakter orientacyjny i są bardzo przybliżone dla innych warunków, ponieważ brakuje jakichkolwiek zależności lub informacji o współoddziaływaniu i charakterze wpływu na współczynnik U wielu innych istotnych czynników.
Badane warianty okien wieloskrzydłowych
W budynkach mieszkalnych rozmiary okien są ograniczone gabarytami pomieszczeń i warunkami bezpieczeństwa. W związku z tym wysokość okien zwykle nie przekracza 1,50 m. Szerokość okien waha się w dużym zakresie, nawet od 0,60 m do 2,40 m. W oknach tych bardzo rzadko stosuje się poziome rygle. Jedynie mogą występować pionowe słupki, tworzące w oknie kilka skrzydeł.
Z uwzględnieniem najczęściej stosowanych rozmiarów okien oraz postawionego celu badania zostały wybrane następujące warianty stolarki okiennej:
- wysokość (stała) - 1,48 m;
- szerokość (zmienna) - od 1,20 m do 1,80 m;
- liczba skrzydeł - do 1 do 3.

RYS. 1-3. Schemat badanych wariantów wieloskrzydłowej stolarki okiennej: jednoskrzydłowe (1), dwuskrzydłowe (2), trzyskrzydłowe (3); rys.: archiwa autorów
Schematy badanych wariantów okien podano na RYS. 1-3.
Do obliczania współczynnika przenikania ciepła stolarki okiennej wieloskrzydłowej najbardziej przydatna i oczywista jest składnikowa metoda oceny, opisana w normie PN-EN ISO 12631:2013-03 [3].
Metoda ta dzieli fragment przegrody na pola powierzchni o różnych właściwościach cieplnych, a całkowitą wartość współczynnika przenikania ciepła oblicza się za pomocą ważonych powierzchniowo wartości U elementów składowych z dodatkowymi członami korekcyjnymi, uwzględniającymi wzajemne oddziaływania cieplne między tymi elementami. Według tej metody dla przyjętych wariantów stolarki okiennej wieloskrzydłowej współczynnik przenikania ciepła Uw należy obliczać zgodnie z równaniem:
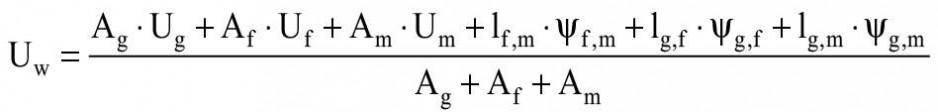 (1)
(1)
gdzie:
- Ug, Uf, Um - współczynniki przenikania ciepła, odpowiednio: oszklenia, ramy, słupków okiennych,
- ψf,m, ψg,f, ψg,m - liniowe współczynniki przenikania ciepła spowodowane połączonymi efektami cieplnymi elementów, odpowiednio: szklącego i ramy, szklącego i słupka, ramy i słupka okiennego,
- lg,f, lg,m, lf,m - długość liniowego mostka cieplnego powstającego na styku, odpowiednio: szkła i ramy, szkła i słupka, ramy i słupka,
- Ag, Am, Af - pole powierzchni, odpowiednio: oszklenia, słupków okiennych, ramy.
Odnosząc się do przedstawionego wzoru (1), autorzy stworzyli algorytm do wyliczania szukanego współczynnika przenikania ciepła okna Uw przy zmianie wartości wybranych czynników, który stanowił podstawę do opracowania modelu matematycznego.
Model matematyczny współczynnika przenikania ciepła okna wieloskrzydłowego
Przy opracowaniu modelu matematycznego dąży się do jego praktycznej utylitarności oraz skuteczności. Takie cechy można osiągnąć, opracowując krótkie modele, w których wykorzystano najważniejsze czynniki interesujące projektantów czy odbiorców stolarki okiennej.
Odwołując się do założonego celu badania, jako funkcję celu przyjęto współczynnik przenikania ciepła wieloskrzydłowej stolarki okiennej Uw [W/(m2·K)].
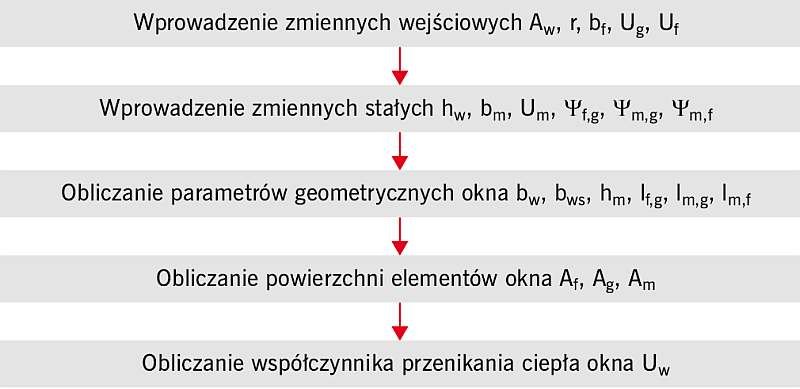
Na RYS. 4 został przedstawiony schemat blokowy wyliczania współczynnika przenikania ciepła okien wieloskrzydłowych.
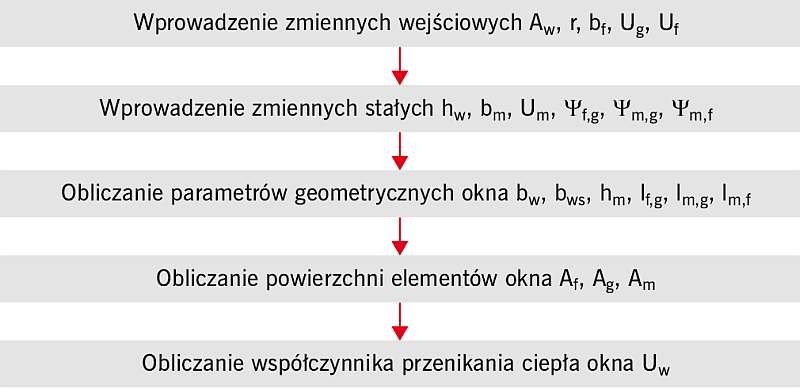
RYS. 4. Schemat blokowy toku postępowania przy obliczaniu współczynnika przenikania ciepła wieloskrzydłowej stolarki okiennej Uw; rys.: archiwa autorów
Zaproponowany algorytm obliczeń został wykorzystany do realizacji eksperymentu obliczeniowego. Wyniki z niego zostały użyte do opracowania deterministycznego modelu matematycznego współczynnika przenikania ciepła stolarki okiennej.
Przypuszczano, że szukaną zależność Y = f (X1, X2, X3, X4, X5) może opisywać wielomian drugiego stopnia.
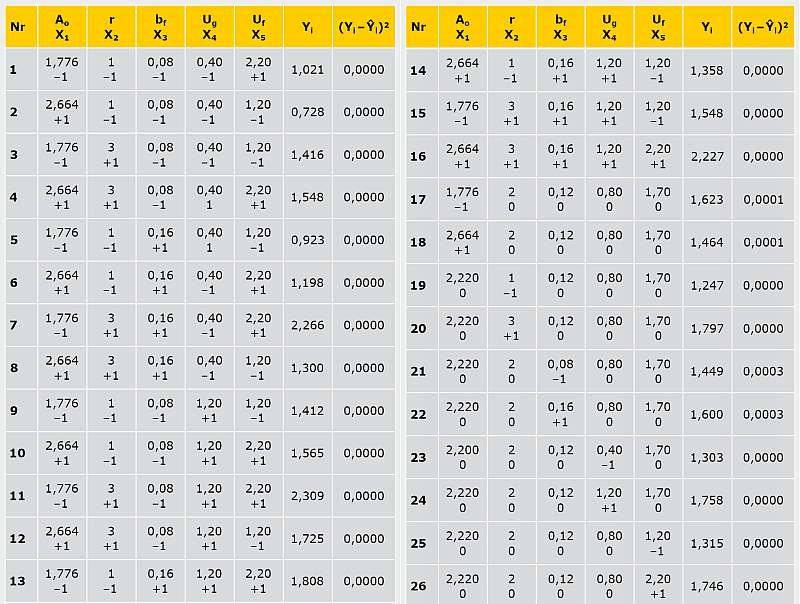
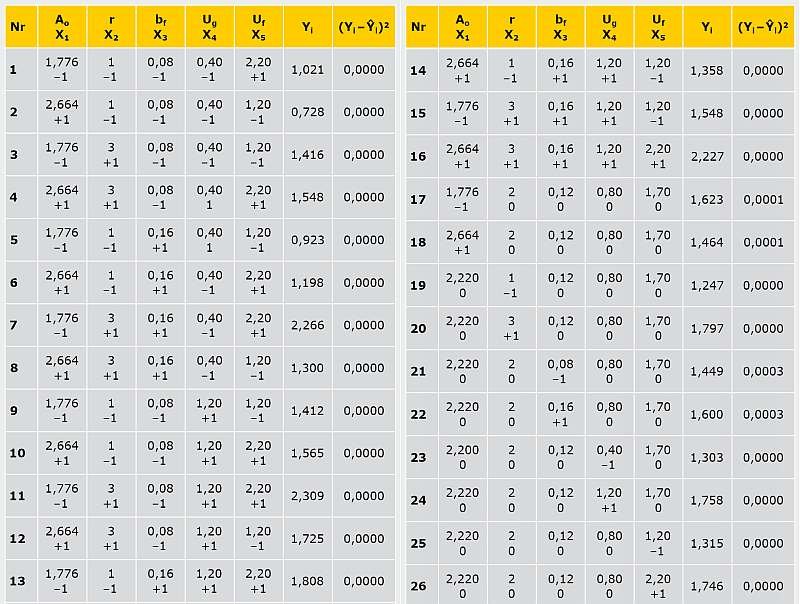
Do uzyskania danych dla opisu tej zależności przeprowadzono 5-czynnikowy eksperyment obliczeniowy według planu drugiego stopnia. Zastosowano kompozycyjny symetryczny trójpoziomowy plan, mający wysoką efektywność statystyczną i zawierający 26 prób [4].
Do wyliczenia wartości Yi w 26 wierszach planu wykorzystano oprogramowanie Microsoft Excel.
Ważnym etapem w badaniu jest wybór zakresu zmienności czynników oraz wartości zmiennych stałych, od których zależą efekty wpływu rozpatrywanych czynników.
Trzeba pamiętać, że zgodnie z obowiązującymi przepisami należy spełnić kilka ważnych warunków:
- Po pierwsze Uw okna od 1 stycznia 2017 r. maksymalnie może wynosić 1,1 W/(m2·K) [5].
- Dodatkowo, jeśli współczynnik Uw dla całkowitego okna jest niższy niż 0,9 W/(m2·K), wówczas wielkość okien i ich liczba jest dowolna.
Jeśli jednak ma on wyższą wartość, należy dostosować się do obowiązujących wymagań i spełnić warunki dotyczące powierzchni przegród przezroczystych w pomieszczeniach.
Wybierając zakres zmienności czynników, takich jak parametry geometryczne okna oraz współczynniki przenikania ciepła dla poszczególnych jego elementów, częściowo opierano się na danych producentów, którzy zaopatrują w stolarkę okienną budynki mieszkalne.
Tak więc pole powierzchni okna Ao (czynnik ![]() ) na średnim poziomie przyjęto równe 1,48×1,50 = 2,220 m2. Górny poziom to powierzchnia okna o 20% większa (1,48×1,80 = 2,664 m2), a dolny o 20% mniejsza (1,48×1,20 = 1,776 m2) od poziomu średniego.
) na średnim poziomie przyjęto równe 1,48×1,50 = 2,220 m2. Górny poziom to powierzchnia okna o 20% większa (1,48×1,80 = 2,664 m2), a dolny o 20% mniejsza (1,48×1,20 = 1,776 m2) od poziomu średniego.
Liczbę skrzydeł w oknach r (czynnik ![]() ) dla budynków mieszkalnych można ograniczyć do 3. Ten czynnik przyjęto na trzech poziomach jako liczby całkowite: 1, 2, 3.
) dla budynków mieszkalnych można ograniczyć do 3. Ten czynnik przyjęto na trzech poziomach jako liczby całkowite: 1, 2, 3.
Szerokość elementów ramy bf (czynnik ![]() ) przyjęto z uwzględnieniem szeroko stosowanych typów stolarki okiennej oraz technologii ich montażu. Wybrano trzy poziomy tego czynnika: 0,08, 0,12, 0,16 m.
) przyjęto z uwzględnieniem szeroko stosowanych typów stolarki okiennej oraz technologii ich montażu. Wybrano trzy poziomy tego czynnika: 0,08, 0,12, 0,16 m.
Jako wartość średnią czynnika Ug (czynnik ![]() ) przyjęto 0,80 W/(m2·K), natomiast na górnym poziomie wybrano wartość równą 1,20 W/(m2·K), a na dolnym równą 0,40 W/(m2·K).
) przyjęto 0,80 W/(m2·K), natomiast na górnym poziomie wybrano wartość równą 1,20 W/(m2·K), a na dolnym równą 0,40 W/(m2·K).
Wartość współczynnika przenikania ciepła ramy Uf (czynnik ![]() ):
):
- na średnim poziomie przyjęto 1,70 W/(m2·K),
- na poziomie najwyższym wybrano wartość równą 2,20 W/(m2·K),
- a najniższa wartość współczynnika Uf przyjęta została na poziomie 1,20 W/(m2·K).
Przy wyborze zakresu zmienności Ug i Uf autorzy opierali się na danych załącznika C do normy PN-EN ISO 10077-1:2007 [6].
Wymienione wartości naturalne czynników ![]() i odpowiadające im wartości unormowane X1, X2, X3, X4, X5 przedstawiono w TAB. 2.
i odpowiadające im wartości unormowane X1, X2, X3, X4, X5 przedstawiono w TAB. 2.
Przejście z wartości naturalnych do unormowanych wyraża się wzorem [4]:
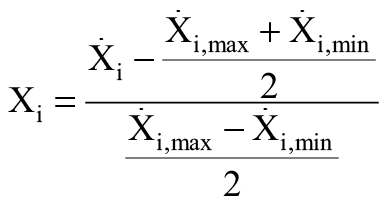 (2)
(2)
gdzie:
Xi, Xi,max, Xi,min - odpowiednio bieżące, maksymalne i minimalne wartości naturalne i-tego czynnika.
Pozostałe zmienne wymienione we wzorze (1) można wyliczyć na podstawie wartości wybranych do modelu czynników zmiennych. Wartość współczynnika przenikania ciepła Um słupków okiennych została przyjęta na tym samym poziomie, co wartość współczynnika przenikania ciepła ramy Uf.
Wartość zmiennej ψf,g przyjęto jako stałą równą 0,080 W/(m·K) według normy PN-EN ISO 14683:2008 [7]. Na podstawie wyników obliczeń (TAB. 1) opracowano równanie regresji zależności Y = f(X1, X2, X3, X4, X5).
Istotność współczynników tego równania oceniono za pomocą t-kryterium. Ponieważ w każdym punkcie planu mamy jeden wynik bez powtórzeń, to wykorzystano podejście, opisane w "Statistische Versuchsplanung und -auswertung in der Stoffwirtschaft" [8], według którego dla każdego współczynnika obliczono tj = |bj|/Sbj, gdzie:
bj - wartości współczynników równania regresji;
Sbj - odchylenie standardowe j-tego współczynnika.
Do określenia Sbj obliczono wariancję S2 na podstawie sumy kwadratów odchyleń (Yi – Ŷi)2. Wartości tj porównywano z wartością krytyczną t0,025;5 = 2,57 [9]. Przy tj < t0,025;5 współczynnik uznawany był jako nieistotny.
Po usunięciu nieistotnych przyjęto postać końcową równania z k+1=15 współczynnikami:
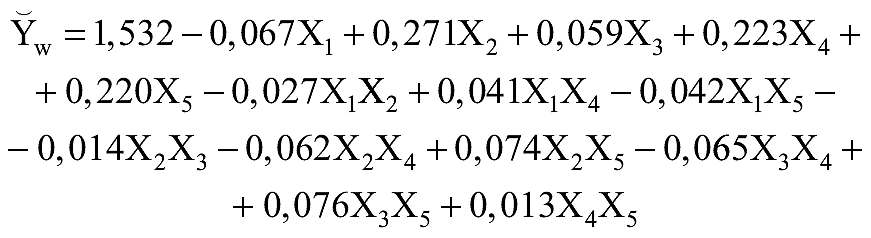 (3)
(3)
Adekwatność modelu, zgodnie z zaleceniami "Statistische Versuchsplanung und -auswertung in der Stoffwirtschaft" [8], oceniono, analizując:
- sumę kwadratów odchyleń Σ(Yi -Ŷi)2;
- wariancję błędów aproksymacji
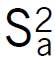 ;
; - współczynnik determinacji R2.
Opracowany model miał:
- Σ(Yi – Ŷi)2 = 0,0011;
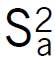 = S(Yi – Ŷi)2/[N – (k+1)] = 0,0002;
= S(Yi – Ŷi)2/[N – (k+1)] = 0,0002;- R2 = 0,9997.
Jakość aproksymacji danych opracowanym równaniem oceniono również według kryterium F [8].
Przy poziomie istotności α = 0,05 i liczbie stopni swobody f1 = N – 1 = 26 – 1 = 25; f2 = N – (k + 1) = 26 – 21 = 5 wartość obliczeniowa kryterium F0 = = 649,5562 wielokrotnie przekracza wartość tabelaryczną F0,05;2;5 = 4,525 [9]. Potwierdza to adekwatność i wysoką jakość opracowanego równania regresji.
Analiza wpływu wybranych parametrów
Na podstawie równania regresji (3) przeanalizowano stopień i charakter wpływu wybranych czynników na współczynnik przenikania ciepła. Analizę przeprowadzono dla zmiennych w postaci naturalnej.
Interesowały nas przede wszystkim parametry okien zapewniające najniższą wartość współczynnika przenikania ciepła Uw. Z równania regresji (3) wykryto, że tylko jeden czynnik - powierzchnia okna Ao (X1) daje wraz ze wzrostem niewielki korzystny wpływ, tj. obniża współczynnik Uw okna. Przy zmianie Ao od 1,776 m2 do 2,664 m2 współczynnik Uw maleje o 8,4%.
Pozostałe czynniki, wraz z ich wzrostem, podnoszą współczynnik Uw.
Przy zmianie wartości tych czynników z poziomu dolnego (–1) do górnego (+1), ich niekorzystne wkłady w podwyższenie Uw wynoszą:
- liczba skrzydeł r (X2) - 43,0%;
- szerokość ramy bf (X3) - 8,0%;
- współczynnik przenikania ciepła oszklenia Ug (X4) - 34,1%;
- współczynnik przenikania ciepła ramy Uf (X5) - 33,5%.
Przy tej analizie warto zaznaczyć, że na każde dodane skrzydło przy średnim poziomie pozostałych czynników współczynnik Uw okna rośnie równomiernie o 21,5%.
Skrupulatna analiza efektów liniowych i współoddziaływań badanych czynników w równaniu regresji (3) pozwoliły wykryć wpływ czynnika X2 (liczba skrzydeł) poprzez jego interakcję na charakter wpływu pozostałych czynników, co zdaniem autorów stanowi najciekawszą część badania.
Oprócz wykrytego faktu, że przejście od jedno- do trójskrzydłowego okna podnosi wartość współczynnika Uw o 43,0%, okazało się, że zmiana liczby skrzydeł jednak wzmacnia korzystny efekt czynnika X1.
Wahania tego czynnika w wybranym zakresie zmienności dla okna jednoskrzydłowego obniżają współczynnik Uw maksymalnie o 6,6%. Natomiast dla okna trójskrzydłowego wahania tego samego czynnika X1 pozwalają obniżyć współczynnik Uw maksymalnie o 9,9%. Wyjaśnić to można wzrostem udziału powierzchni szklonej w oknach większych rozmiarów.
Wzrost liczby skrzydeł osłabia niekorzystny wpływ czynników X3 i X4 na współczynnik Uw.
Dla okna jednoskrzydłowego maksymalny wzrost Uw przy wahaniach czynnika X3 w wybranym zakresie zmienności wynosi 12,3%, natomiast przy wahaniach czynnika X4 - 58,4%.
Dla okna trójskrzydłowego wahania tych czynników podwyższają współczynnik Uw maksymalnie 5,1% (X3) oraz 19,6% (X4). Mocne współoddziaływanie liczby skrzydeł przejawia się w stosunku do czynnika X5. Wzrost liczby skrzydeł, niestety, wzmacnia niekorzystny wpływ tego czynnika.
Dla okna jednoskrzydłowego maksymalny wzrost Uw przy wahaniach czynnika X5 w wybranym zakresie zmienności wynosi 26,2%; dla okna trójskrzydłowego wahania tego czynnika podwyższają współczynnik Uw maksymalnie o 39,0%. Związane to jest z istotnym wzrostem powierzchni ramy w oknach o trzech skrzydłach, co odbija się na wzmocnieniu wkładu ramy w pogorszenie współczynnika Uw.
Opisany charakter wpływu czynników odzwierciedlają również wykresy na RYS. 5-6 i RYS. 7-8, na których pokazano graficzne zależności Uw = f (Ao,Ug) oraz Uw = f (bf, Uf) dla r = 1 oraz r = 3, wykonane w systemie współrzędnych 3D.
![RYS. 5-6. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od powierzchni okna Ao [m2] i współczynnika przenikania ciepła szyby Ug [W/(m2·K)] przy liczbie skrzydeł okiennych: r = 1 (5), r = 3 (6); rys.: archiwa autorów RYS. 5-6. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od powierzchni okna Ao [m2] i współczynnika przenikania ciepła szyby Ug [W/(m2·K)] przy liczbie skrzydeł okiennych: r = 1 (5), r = 3 (6); rys.: archiwa autorów](https://www.izolacje.com.pl/media/cache/typical_view/data/202012/b-parametry-cieplne-wieloskrzydlowej-stolarki-rys5-6.jpg)
RYS. 5-6. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od powierzchni okna Ao [m2] i współczynnika przenikania ciepła szyby Ug [W/(m2·K)] przy liczbie skrzydeł okiennych: r = 1 (5), r = 3 (6); rys.: archiwa autorów
![RYS. 7-8. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od szerokości ramy bf [m]; rys.: archiwa autorów RYS. 7-8. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od szerokości ramy bf [m]; rys.: archiwa autorów](https://www.izolacje.com.pl/media/cache/typical_view/data/202012/b-parametry-cieplne-wieloskrzydlowej-stolarki-rys7-8.jpg)
RYS. 7-8. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od szerokości ramy bf [m]; rys.: archiwa autorów
W wyniku optymalizacji równania regresji (3) wykryto, że uzyskana funkcja osiąga minimalną (najlepszą) wartość Uw,min = 0,728 W/(m2·K) przy następujących wartościach czynników:
Ao = 2,664 m2;
r = 1;
bf = 0,08 m;
Ug =0,40 W/(m2·K);
Uf = 1,20 W/(m2·K).
Natomiast maksymalną (najgorszą) wartość Uw,max = 2,403 W/(m2·K) obserwuje się przy:
Ao = 1,776 m2
r = 3;
bf = 0,16 m;
Ug = 1,20 W/(m2·K);
Uf = 2,20 W/(m2·K).
Opracowany model matematyczny dla zbioru dowolnych wartości zbadanych czynników (z przyjętych w tym badaniu zakresów zmienności) po ich unormowaniu według wzoru (2) pozwala obliczyć współczynnik przenikania ciepła wieloskrzydłowej stolarki okiennej dowolnej z wybranych konfiguracji. Model również może być wykorzystany do numerycznego sterowania obiektem badania.
Wnioski
Za pomocą opracowanego deterministycznego modelu matematycznego przeanalizowano charakter i stopień wpływu podstawowych czynników w wybranym zakresie ich zmienności na współczynnik przenikania ciepła Uw wieloskrzydłowej stolarki okiennej.
Wykryto, że na współczynnik Uw korzystny wpływ wykazuje jedynie powierzchnia okna Ao. Przy zmianie Ao od 1,776 do 2,664 m2 wartość współczynnika Uw maleje o 8,4%. Wraz ze wzrostem pozostałych czynników, współczynnik Uw rośnie.
Na charakter i stopień wpływu czynników nakłada się współoddziaływanie czynnika r (X2) - liczby skrzydeł w oknie, który istotnie koryguje oddziaływanie pozostałych czynników.
Ustalono, że optymalne wartości zbadanych parametrów dla wieloskrzydłowej stolarki okiennej to:
Ao = 2,664 m2;
r =1;
bf = 0,08 m;
Ug = 0,40 W/(m2·K);
Uf = 1,20 W/(m2·K).
Pozwalają one osiągnąć minimalną wartość współczynnika Uw,min = 0,728 W/(m2·K).
Opracowany model matematyczny pozwala dla zbioru dowolnych wartości zbadanych czynników (z przyjętych dla nich zakresów zmienności) po ich unormowaniu obliczyć współczynnik przenikania ciepła wieloskrzydłowej stolarki okiennej.
Literatura
- W. Jezierski, J. Borowska, "Analiza parametrów cieplnych współczesnej stolarki okiennej", "IZOLACJE", nr 4/2017.
- Strona internetowa: www.cieplej.pl.
- PN-EN ISO 12631:2013-03, "Cieplne właściwości użytkowe ścian osłonowych. Obliczanie współczynnika przenikania ciepła".
- Z. Polański, "Planowanie doświadczeń w technice", PWN, Warszawa 1984.
- Rozporządzenie Ministra Infrastruktury z dnia 12 kwietnia 2002 r. w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie z późniejszymi aktualizacjami.
- PN-EN ISO 10077-1:2007, "Cieplne właściwości użytkowe okien, drzwi i żaluzji. Obliczanie współczynnika przenikania ciepła. Część 1: Metoda uproszczona".
- PN-EN ISO 14683:2008, "Mostki cieplne w budynkach. Liniowy współczynnik przenikania ciepła. Metody uproszczone i wartości orientacyjne".
- K. Hartmann, E. Lezki, W. Schär, "Statistische Versuchsplanung und –auswertung in der Stoffwirtschaft", VEB, Leipzig 1977.
- W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska, M. Wasilewski, "Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach. Część II. Statystyka matematyczna", PWN, Warszawa 2003.




![RYS. 5–6. Zależność współczynnika przenikania ciepła
stolarki okiennej U<sub>w</sub> [W/(m<sup>2</sup>·K)] od powierzchni okna A<sub>o</sub> [m<sup>2</sup>] i współczynnika
przenikania ciepła szyby U<sub>g</sub> [W/(m<sup>2</sup>·K)] przy liczbie skrzy.](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/parametry-cieplne-wieloskrzydlowej-stolarki-rys5-6.jpg)
![RYS. 7–8. Zależność współczynnika przenikania ciepła
stolarki okiennej U<sub>w</sub> [W/(m<sup>2</sup>·K)] od szerokości ramy b<sub>f</sub> [m]; rys.: archiwa autorów (W. Jezierski, J. Borowska)](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/parametry-cieplne-wieloskrzydlowej-stolarki-rys7-8.jpg)
![TABELA 1. Współczynnik przenikania ciepła okna składającego się z różnej ilości kwater [2]](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/parametry-cieplne-wieloskrzydlowej-stolarki-tab1.jpg)