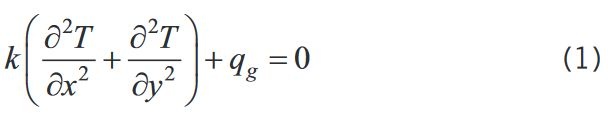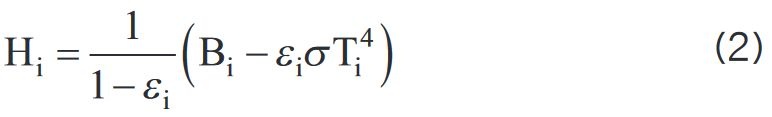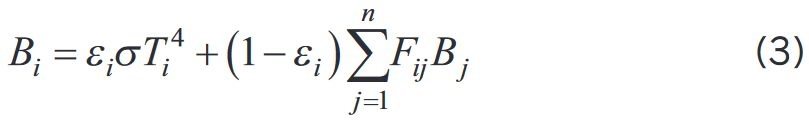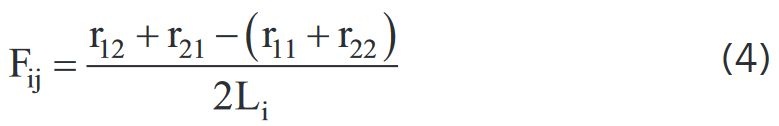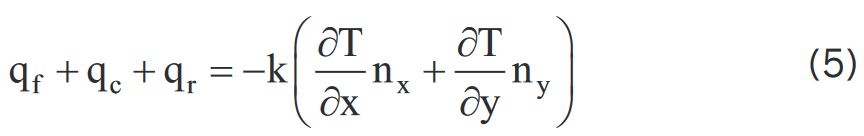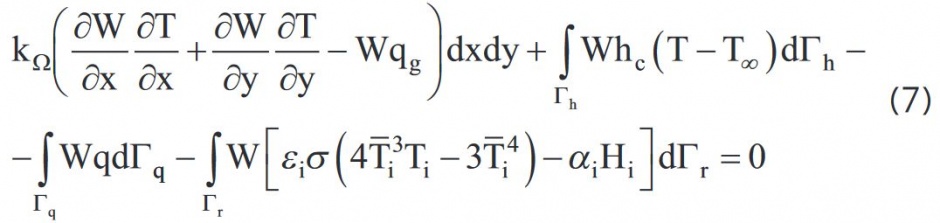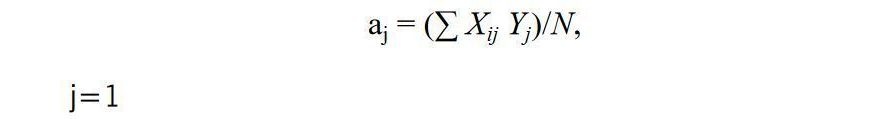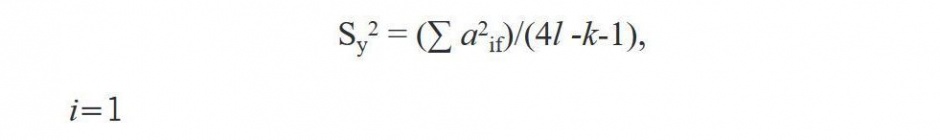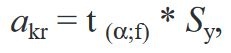Określenie istotności wpływu parametrów węzła połączenia płyty balkonowej ze ścianą na pole temperatur
Determining the significance of the influence of the parameters of the junction node of the balcony slab with the wall the temperature field
![Zdjęcie termowizyjne węzła balkonowego połączonego ze ścianą, rys. [2]](https://www.izolacje.com.pl/media/cache/typical_view/data/202308/rys0-laczniki-1.jpg)
Zdjęcie termowizyjne węzła balkonowego połączonego ze ścianą, rys. [2]
Balkon ma wiele zalet, wpływa on pozytywnie na walory estetyczne budynku, zwiększa przestrzeń użytkową, jest dobrym miejscem na odpoczynek i relaks, daje możliwość uprawy roślin. W wysokich budynkach pełni funkcję niezwykłych punktów widokowych, a ponadto zwiększa wartość nieruchomości.
Zobacz także
mgr inż. Maciej Rokiel Okapy balkonów i tarasów – poprawne rozwiązania materiałowo‑technologiczne

Balkon czy taras to element konstrukcyjny budynku powiększający w niewątpliwy sposób jego wartość użytkową. Możliwości jego wykorzystania są ogromne, od miejsca przeznaczonego na wypoczynek, do przedłużenia...
Balkon czy taras to element konstrukcyjny budynku powiększający w niewątpliwy sposób jego wartość użytkową. Możliwości jego wykorzystania są ogromne, od miejsca przeznaczonego na wypoczynek, do przedłużenia np. salonu. Aby jednak ten modny (i chyba dobrze) obecnie element nie sprawiał użytkownikowi problemów, konieczne jest pokonanie dość niełatwych problemów, zarówno projektowych, jak i wykonawczych.
mgr inż. Maciej Rokiel Odprowadzanie wody z połaci balkonów i tarasów. Wybrane zagadnienia

Konieczność szybkiego i skutecznego odprowadzenia wody opadowej z balkonu czy tarasu to podstawa komfortowego użytkowania połaci.
Konieczność szybkiego i skutecznego odprowadzenia wody opadowej z balkonu czy tarasu to podstawa komfortowego użytkowania połaci.
Czytaj całość »
Alchimica Polska Sp. z o.o. Hydroizolacja tarasu i balkonu w systemie Hyperdesmo
Zarówno balkon, jak i taras cały czas są narażone na działanie destrukcyjnych czynników atmosferycznych. Dlatego też zastosowane podczas ich budowy materiały przede wszystkim muszą stanowić skuteczną ochronę...
Zarówno balkon, jak i taras cały czas są narażone na działanie destrukcyjnych czynników atmosferycznych. Dlatego też zastosowane podczas ich budowy materiały przede wszystkim muszą stanowić skuteczną ochronę przed wodą, wilgocią i zmianami temperatury. I to niezależnie od wielkości tych przydomowych powierzchni.
Czytaj całość »*****
W artykule przedstawiono wyniki analizy istotności wpływu parametrów węzła połączenia płyty balkonowej ze ścianą na pole temperatur w strefie powstającego mostka termicznego.
Węzeł składa się z dużej liczby elementów, które mają zróżnicowane wartości współczynnika przewodzenia ciepła, wymiary geometryczne i lokalizację odnośnie do wewnętrznej powierzchni ściany zewnętrznej.
Najbardziej zagrażającymi miejscami są górne i dolne narożniki, utworzone ze stropem i ścianą zewnętrzną.
Po analizie charakterystyk fizyko-technicznych i geometrycznych elementów wybranego węzła wyodrębniono 12 czynników ( Xi ), które mogą mieć wpływ na pole temperatur ściany zewnętrznej.
Oceniono istotność wpływu wybranych czynników ( Xi ) na temperaturę powierzchni wewnętrznej w narożniku górnym, przyjętej jako funkcja celu Y1 , oraz w narożniku dolnym, przyjętej jako funkcja celu Y2 .
Do oceny istotności zastosowano eksperyment obliczeniowy z planowaniem Placketta-Burmana na N =16 prób. Na podstawie wyników obliczeń temperatur Y1 , Y2 określono współczynniki istotności dla wybranych czynników.
Po analizie istotności czynników ustalono, że temperatura Y2 ( ϑimd ) na wewnętrznej powierzchni ściany zewnętrznej na styku z dolną częścią stropu jest krytyczna w rozpatrywanym węźle.
Okazało się, że wśród wybranych 12 czynników istotny wpływ na temperaturę Y2 ( ϑimd ) wykazuje sześć czynników, a pozostałe czynniki mają wpływ nieistotny.
Przy optymalizacji parametrów rozpatrywanego węzła według kryterium temperaturowego należy uwzględniać wytypowane czynniki istotne. Informacja może być przydatna dla naukowców, projektantów i technologów w budownictwie.
Determining the significance of the influence of the parameters of the junction node of the balcony slab with the wall the temperature field
The article presents the results of the analysis of the significance of the influence of the parameters of the connection node of the balcony slab with the wall on the temperature field in the zone of the emerging thermal bridge.
The node consists of a large number of elements that have different values of the heat conduction coefficient, geometric dimensions and location relative to the inner surface of the outer wall.
The most threatening places are the upper and lower corners, formed by the ceiling and the outer wall.
After analyzing the physical, technical and geometric characteristics of the selected node, 12 factors ( Xi ) were identified that can affect the temperature field of the outer wall. The significance of the influence of selected factors ( Xi ) on the internal surface temperature in the upper corner, taken as a function of the target Y1, and in the lower corner, taken as a function of the target Y2 was assessed.
A computational experiment with Plackett-Burman planning on N =16 samples was used to assess the significance. Based on the results of calculations of temperatures Y1, Y2, the significance factors for the selected factors are determined.
After analyzing the significance of the factors, it was determined that the temperature Y2 ( ϑimd ) on the inner surface of the outer wall in contact with the ceiling from the bottom of the ceiling is critical at the node under consideration.
It turned out that among the selected 12 factors, six factors have a significant effect on the temperature of Y2 ( ϑimd ), the remaining factors have an insignificant effect.
When optimizing the parameters of the node under consideration according to the temperature criterion, the selected important factors should be taken into account. The information can be useful for scientists, designers and technologists in construction.
*****
Ze względu na konstrukcję balkony mogą być [1]:
- wspornikowe – utwierdzane w ścianach nośnych lub stropach, w sposób zapewniający im odpowiednie zakotwienie (RYS. 1),
- podwieszane – mocowane są one do ścian konstrukcyjnych za pomocą stalowych konstrukcji lub cięgien stalowych z zastrzałami i belkami od spodu płyty (RYS. 2),
- podparte – oparte na konstrukcji dostawionej do budynku i usytuowanej na oddzielnym fundamencie, połączenie ze ścianą zapewniają najczęściej kotwy z kształtowników stalowych, które pozytywnie oddziaływają na zachowanie stateczności oraz przeniesienie obciążeń poziomych od wiatru (RYS. 3).
Poznaj działanie: Płynnych membran do naprawy balkonów i tarasów
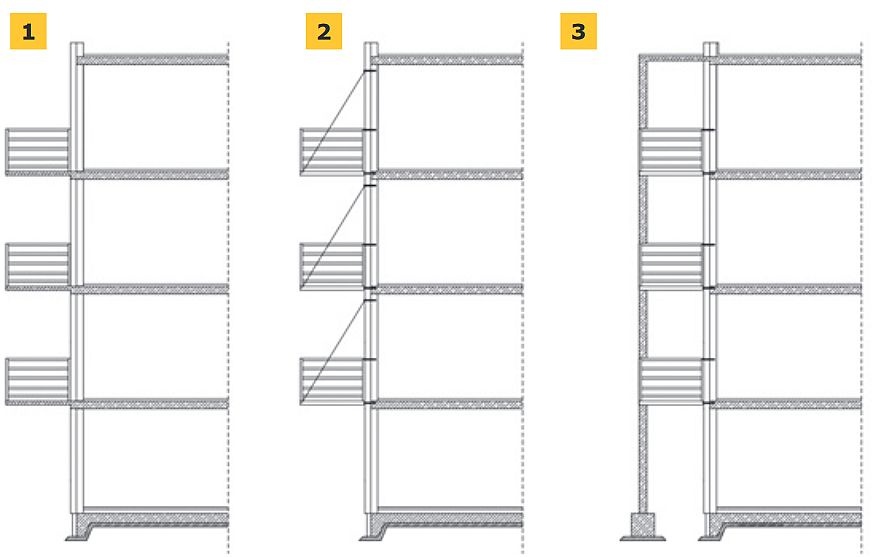
RYS. 1–3. Podział balkonów ze względu na konstrukcję: wspornikowy (1), podwieszany (2), podparty (3); rys.: W. Jezierski, C. Leszczyński
Natomiast ze względu na właściwości użytkowe wyróżniamy balkony [ 1 ]:
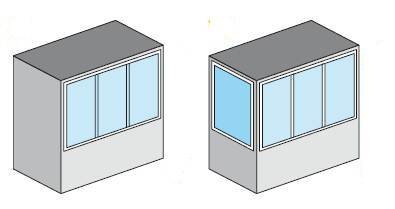
- klasyczne – wiszący, najczęściej spotykany, wystający poza fasadę budynku (RYS. 4),
- francuskie – jest to w praktyce bardziej element architektoniczny niż miejsce użytkowe, charakteryzuje się przeszkleniem całej powierzchni, która jest zabezpieczona barierkami ochronnymi (RYS. 5),
- loggie – może być wysunięta poza obrys fasady lub być w jej części jako wnęka, jej przewaga nad klasycznym balkonem polega na tym, że loggia ma osłoniętą przestrzeń w całości lub częściowo, która pełni funkcję ochronną przed deszczem czy wiatrem (RYS. 6).
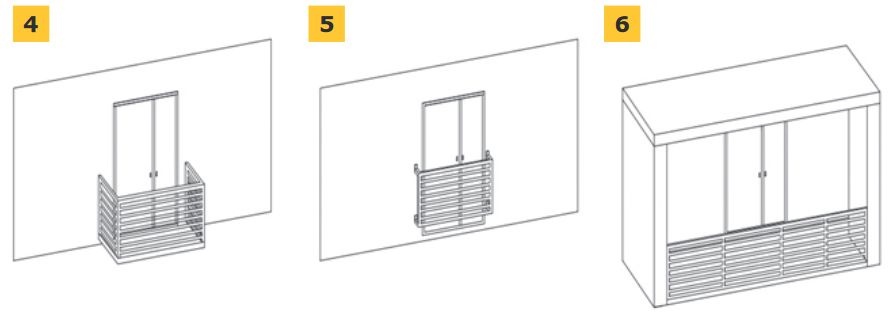
RYS. 4–6. Podział balkonów ze względu na właściwości użytkowe: klasyczny (4), francuski (5), loggia (6); rys.: W. Jezierski, C. Leszczyński
Mimo wielu zalet, balkon jest miejscem newralgicznym. Problem polega na trudności zapewnienia ciągłości ocieplenia ścian zewnętrznych w miejscu występowania balkonu. Wzdłuż całej jego długości występowania generuje się mostek termiczny, który można wykryć za pomocą kamer termowizyjnych ( RYS. 7 ) [ 2 ]. Wygenerowany zapis z kamer termowizyjnych, zwany termogramem, pokazuje wszystkie miejsca uchodzenia ciepła. Barwa czerwona/pomarańczowa odpowiada miejscom cieplejszym. Miejsca chłodne oznaczone są przez kolor niebieski/granatowy.
Skutkiem mostka termicznego jest obniżenie temperatury miejsca styku ściany zewnętrznej z górną i dolną częścią stropu. Taki stan rzeczy wpływa na pogorszenie komfortu cieplnego użytkowników danego budynku. Nie rzutuje to w istotnym stopniu na cały budynek, jednak w strefie zamocowania płyty balkonowej może powstać zjawisko kondensacji pary wodnej, doprowadzając do zawilgocenia muru. To niepożądane zjawisko prowadzi do spadku izolacyjności termicznej, odspojenia tynków, rozwoju grzybów pleśniowych oraz powstawania zapachu stęchlizny.
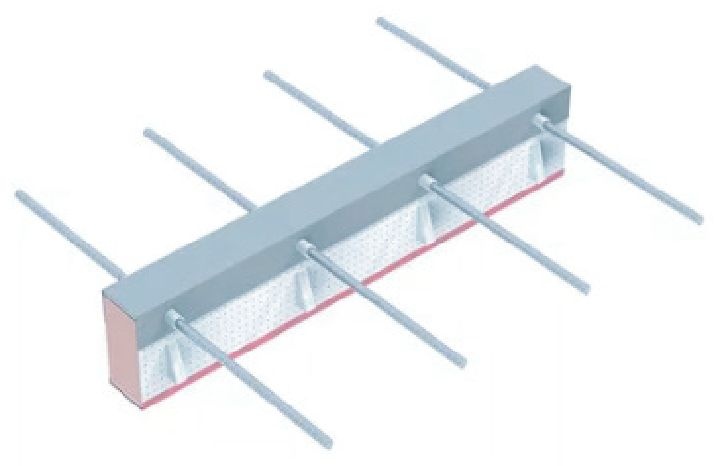
Najbardziej powszechnym rozwiązaniem tego problemu jest stosowanie specjalistycznych łączników w postaci prefabrykowanych elementów zbrojeniowych [ 3 ]. W obszarze materiału izolacyjnego wykonane są one ze stali szlachetnej, która charakteryzuje się niższą przewodnością cieplną. Najczęściej wykorzystywany materiał izolacyjny w łącznikach to wełna mineralna lub szary polistyren ( RYS. 8 ). Na rynku dostępnych jest wiele łączników, które można dopasować do indywidualnych projektów w zależności od preferencji i potrzeb.
Innym z rozwiązań problemu pojawiającego się mostka termicznego na połączeniu balkonu ze ścianą i stropem jest ocieplenie płyty balkonowej wzdłuż wszystkich krawędzi materiałem termoizolacyjnym o jak najniższym współczynniku przewodzenia ciepła. Grubość izolacji termicznej na balkonach projektowana jest indywidualnie przez projektantów, jednak zazwyczaj waha się ona w granicach od 5 do 10 cm.
W budynkach istniejących znacznym ograniczeniem będzie grubość materiału izolacyjnego ze względu na występujące progi drzwi balkonowych. W budynkach projektowanych taki zabieg prowadzi do zwiększenia w znacznym stopniu grubości płyty balkonowej. Obecnie na rynku materiałem o najniższym współczynniku przewodzenia ciepła jest płyta PIR λ = 0,019–0,023 W/(m·K). Względem zwykłego styropianu EPS, a nawet jego udoskonalonej wersji XPS płyta PIR może być użyta o grubości około dwa razy mniejszej przy zachowaniu jednakowych właściwościach fizycznych.
Problem występowania mostków termicznych balkonu wspornikowego połączonego ze ścianą zewnętrzną i stropem analizował dr inż. K. Pawłowski [ 4 ].
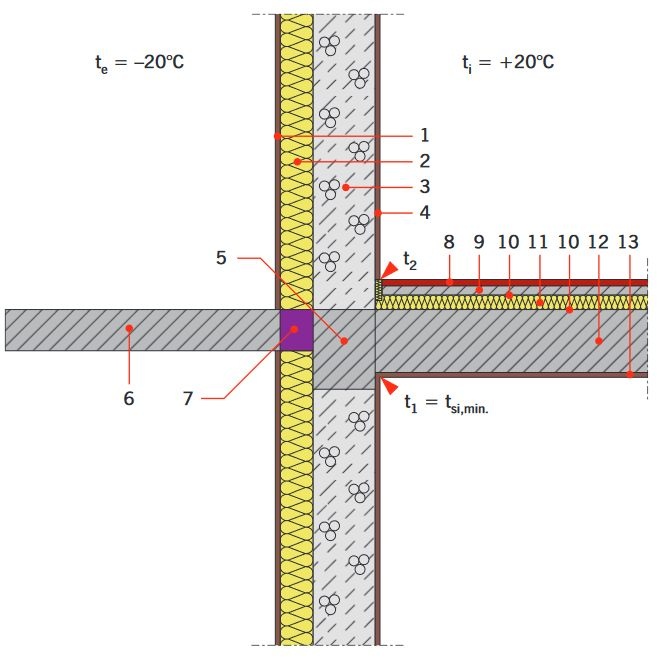
RYS. 9. Rozwiązanie konstrukcyjno-materiałowe płyty balkonowej ze ścianą i stropem przy użyciu łącznika izotermicznego. Objaśnienia: 1 – tynk cienkowarstwowy gr. 0,5 cm, 2 – płyty styropianowe gr. 12 lub 20 cm, w zależności od wariantu obliczeniowego, 3 – bloczki z betonu komórkowego gr. 24 cm, 4 – tynk gipsowy gr. 1,5 cm, 5 – wieniec żelbetowy o wymiarach 24x30 cm, 6 – płyta żelbetowa gr. 16 cm, 7 – łącznik izotermiczny gr. 12 cm, 8 – parkiet drewniany gr. 2 cm, 9 – gładź cementowa gr. 3 cm, 10 – folia polietylenowa, 11 – płyty styropianowe gr. 5 cm, 12 – strop gęstożebrowy gr. 24 cm, 13 – tynk gipsowy gr. 1,5 cm; rys.: [4]
Jak wykazały wyniki obliczeniowe, największy pozytywny wpływ na minimalną temperaturę złącza na wewnętrznej powierzchni przegrody ma łącznik izotermiczny. Ponadto należy zauważyć, że na pole temperatur oraz na temperaturę wewnętrznej powierzchni złącza wpływa duża liczba czynników. W skład węzła wchodzi 13 materiałów ( RYS. 9 ), którym odpowiadają parametry geometryczne, parametry fizyczne oraz przypisana jest ich lokalizacja w węźle.
W pracy [ 5 ] dr inż. M. Grudzińska również przeanalizowała węzły płyt balkonowych. Autorka przestudiowała następujące rozwiązania konstrukcyjno-materiałowe: ocieplenie płyty balkonowej wzdłuż wszystkich krawędzi, zastosowanie izolowanych wkładek zbrojeniowych, oddylatowanie płyty balkonowej od budynku. W tym przypadku rozwiązanie z zastosowaniem oddylatowanej płyty balkonowej okazało się najbardziej korzystnym ze względu na minimalną temperaturę na wewnętrznej powierzchni złącza ( RYS. 10 ). Po raz kolejny można zauważyć, że na pole temperatur oraz na temperaturę wewnętrznej powierzchni złącza wpływa duża liczba czynników. W tym przypadku w skład węzła wchodzi dziewięć materiałów o różnych właściwościach.
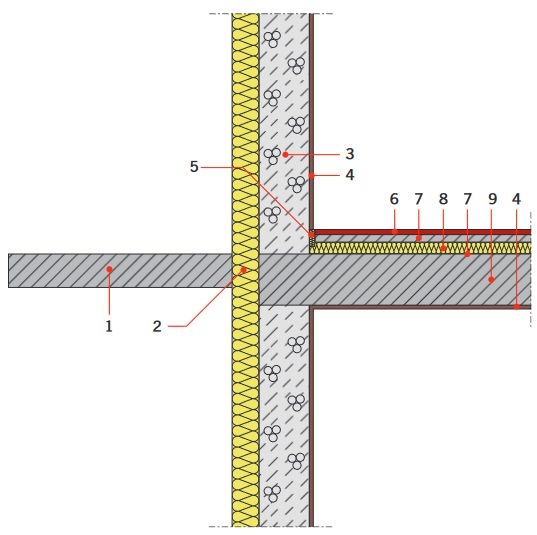
RYS. 10. Rozwiązanie konstrukcyjno-materiałowe oddylatowanej płyty balkonowej od budynku. Objaśnienia: 1 – płyta balkonowa żelbetowa, 2 – ocieplenie ściany zewnętrznej płytami styropianowymi, 3 – ściana zewnętrzna wykonana z gazobetonu o gęstości 700 kg/m3, 4 – tynk, 5 – styropian oddylatowujący szlichtę betonową od ściany, 6 – szlichta betonowa, 7 – folia polietylenowa, 8 – ocieplenie stropu od góry płytami styropianowymi, 9 – strop żelbetowy gr. 24 cm; rys.: [5]
Jak widać w przytoczonych badaniach autorzy operowali dużą liczbą czynników wpływających na pole temperatur. Można zauważyć, że liczba ta wynika z sumy poszczególnych materiałów kontaktujących w analizowanym węźle. Jednak całkowita liczba zmiennych dla każdego materiału w tych węzłach zwiększa się dwu- lub trzykrotnie, ponieważ każdy materiał powinien być scharakteryzowany przez wymiary geometryczne, właściwości fizyczne i jego lokalizację. Przy takiej liczbie występujących czynników optymalizacja rozwiązań węzłów według kryterium temperaturowego jest bardzo problematyczna.
Przy analizie podobnych systemów technicznych, w których na badaną cechę oddziałuje duża liczba czynników, powstaje konieczność wyeliminowania czynników nieistotnych. Do realizacji eksperymentów w celu wyeliminowania czynników nieistotnych stosuje się specjalne plany, zmniejszające pracochłonność badań i upraszczających opracowanie wyników. Spośród skutecznych metod wyróżnia się plany ortogonalne nasycone dwupoziomowe D-optymalne Placketta-Burmana, umożliwiające dokonanie oceny istotności wpływu do kilkudziesięciu czynników wejściowych. Te plany są odpowiednim narzędziem do badań istotności wpływu parametrów węzła połączenia płyty balkonowej ze ścianą na pole temperatur w strefie powstającego mostka termicznego. Ortogonalne plany zapewniają maksymalną dokładność przy określeniu liniowych efektów czynników, a także jednakową dokładność dla wszystkich analizowanych czynników [ 6 ].
W związku z powyższym, celem danego badania jest analiza istotności wpływu parametrów węzła połączenia płyty balkonowej ze ścianą na pole temperatur w strefie powstającego mostka termicznego z wyeliminowaniem czynników nieistotnych. Analizę przewiduje się wykonać na podstawie realizacji eksperymentu obliczeniowego zaplanowanego według planu Placketta-Burmana na 15 czynników.
Opis obiektu badania
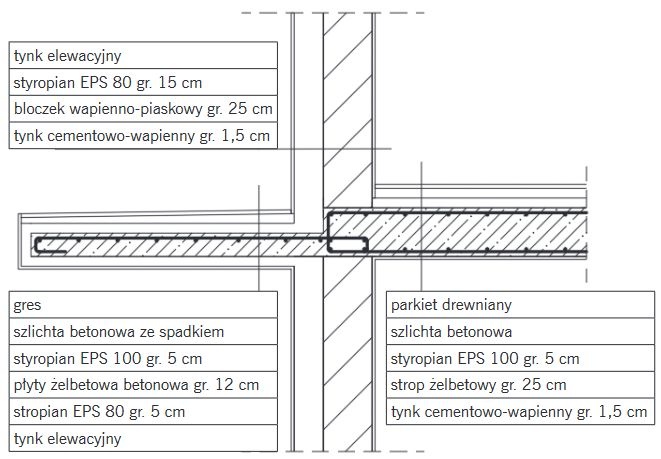
RYS. 11. Połączenie monolityczne płyty balkonowej ze stropem – płyta balkonowa jako przedłużenie stropu względem dolnej krawędzi; rys.: W. Jezierski, C. Leszczyński
Badanie przeprowadzono dla węzła połączenia żelbetowej płyty balkonowej ze stropem żelbetowym oraz ścianą murowaną wykonaną z bloczku wapienno-piaskowego ( RYS. 11–12 ). Izolację termiczną przyjęto ze względu na dostępność materiałów na rynku budowlanym, uwzględniając te, które charakteryzują się najlepszymi i względnie najgorszymi parametrami fizycznymi. Jako materiał z najlepszym współczynnikiem przewodzenia ciepła zastosowano płytę PIR wykonaną ze sztywnej pianki poliizolacyjnej, natomiast jako materiał z najsłabszym współczynnikiem przewodzenia ciepła – styropian EPS.
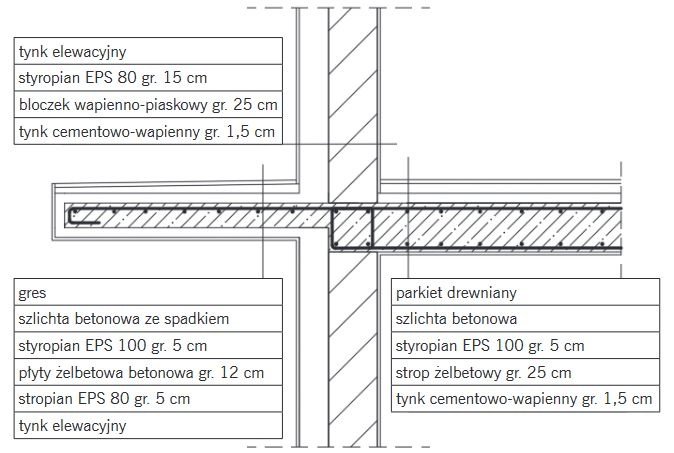
RYS. 12. Połączenie monolityczne płyty balkonowej ze stropem – płyta balkonowa jako przedłużenie stropu względem górnej krawędzi; rys.: W. Jezierski, C. Leszczyński
Płyta balkonu w tradycyjnej wersji to przedłużenie płyty stropowej. Płyta balkonowa zalewana jest równocześnie ze stropem i razem z nim rozszalowywana. Taki wariant gwarantuje dowolność architektoniczną, a jedynym ogranicznikiem jest minimalna grubość płyty – 8 cm [7 ]. Przyjęto w badaniu konstrukcję wspornikową, czyli przedłużenie stropu poza obrys budynku. Płyta kotwiona jest za pomocą górnej siatki zbrojeniowej wyprowadzonej ze stropu. Dozwolone jest przedłużenie płyty względem dolnej krawędzi stropu, jak i górnej (RYS. 11–12 ).
Tok postępowania przy określeniu pól temperatur w obrębie powstającego mostka termicznego
Pole temperaturowe określono za pomocą programu THERM 7,6 [8], który umożliwia:
- modelowanie skomplikowanych dwuwymiarowych modeli obliczeniowych,
- analizowanie parametrów cieplnych przegród budowlanych,
- analizowanie wymiany ciepła metodą MES – metoda elementów skończonych.
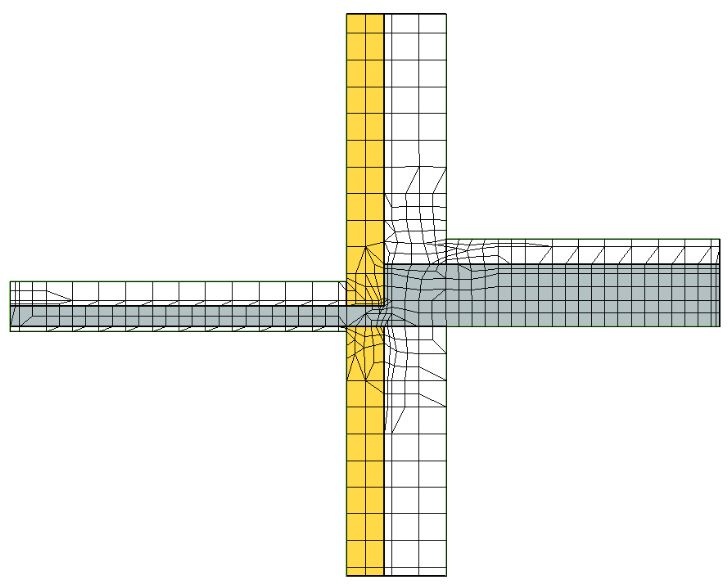
RYS. 13. Wytworzona siatka elementów skończonych jednego z analizowanych wariantów węzła; rys.: oprac. W. Jezierski, C. Leszczyński przy użyciu oprogramowania Therm 7.6
Program THERM bazuje na metodzie elementów skończonych (MES). Za pomocą metody MES obliczane są wytrzymałości konstrukcji, odkształcenia, naprężenia, przemieszczenia, przepływy ciepła oraz cieczy. Rozpoczynając obliczenia, w pierwszej kolejności należy określić geometrię badanego obszaru. W programie THERM przekrój poprzeczny analizowanego elementu można zamodelować bezpośrednio w nim lub nanieść wcześniej przygotowany plik w formacie DXF.
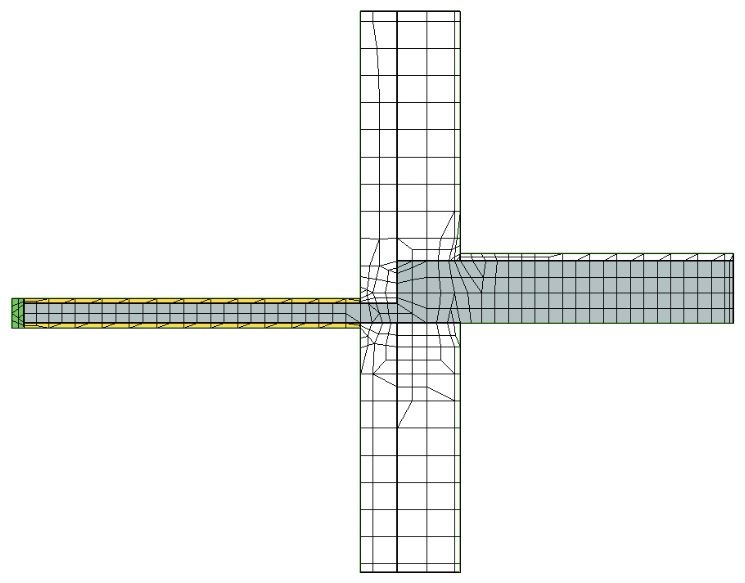
RYS. 14. Rozłożenie izoterm w jednym z analizowanych wariantów złącza; rys.: oprac. W. Jezierski, C. Leszczyński przy użyciu oprogramowania Therm 7.6
Po zakończeniu modelowania określa się warunki brzegowe. Polega to na definicji właściwości materiału dla każdego wielokąta oraz na wprowadzeniu warunków środowiskowych, które mają wpływ na poszczególne części analizowanego węzła.
W celu prawidłowego zdefiniowania modelu należy nadać warunki brzegowe dla wszystkich powierzchni brzegowych.
Kolejnym krokiem jest nadanie parametrów fizykochemicznych badanego węzła. Program THERM wyposażony jest w wewnętrzną bibliotekę materiałów. Jednak nie znajdują się tam wszystkie materiały budowlane dostępne na rynku. W takiej sytuacji należy samodzielnie stworzyć materiały za pomocą narzędzi wewnętrznych, które oferuje program.
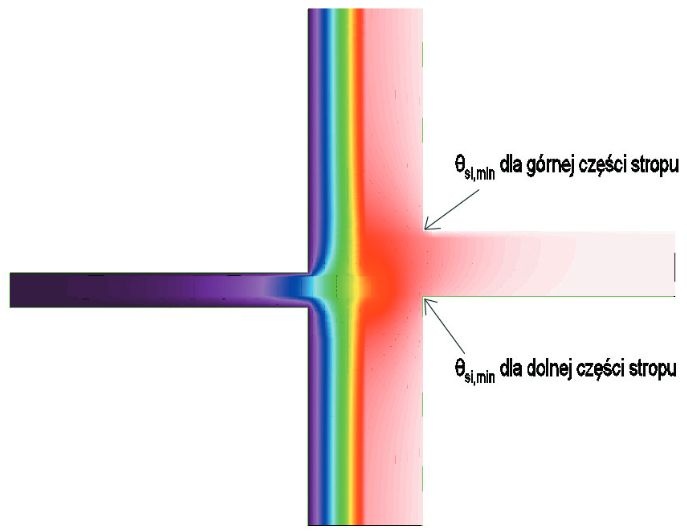
RYS. 15. Miejsce występowania najniższych temperatur ściany wewnętrznej w okolicy występowania balkonów w jednym z analizowanych wariantów złącza; rys.: oprac. W. Jezierski, C. Leszczyński przy użyciu oprogramowania Therm 7.6
Ostatnim krokiem jest definicja siatki elementów skończonych, która wypełnia w całości obszar poddany analizie ( RYS. 13 ). W wyniku obliczeń możemy otrzymać wartość współczynnika przenikania ciepła U , rozkład izoterm ( RYS. 14 ), rozkład wektorów strumienia ciepła oraz wartość pola temperaturowego (lokalnej, średniej, maksymalnej i minimalnej ( RYS. 15 ).
Program THERM oblicza wartości na podstawie kierunków przepływu ciepła, emisyjności powierzchniowej, geometrii modelu oraz temperatury. Symulacja numeryczna trwa do momentu aż żaden z lokalnych regionów nie wykaże poziomu błędu obliczeniowego wyższego niż zalecany.
Metoda określenia pól temperatur w obrębie powstającego mostka termicznego
Równanie określające dwuwymiarowe przewodzenie ciepła, zgodnie z założeniem o stałych właściwościach fizycznych, wyprowadza się z ogólnego równania energii [ 9 ], w wyniku czego powstaje równanie różniczkowe cząstkowe:
gdzie:
W programie THERM dla warunków brzegowych segmenty powierzchni z założenia są szare i izotermiczne, dlatego α = ε.
Równanie napromieniowania H ma postać:
gdzie:
B – promienistość powierzchni, obliczana za pomocą równania:
Za pomocą reguły krzyżowej obliczane są współczynniki widoku F (4):
Za pomocą prawa Fouriera określana jest wielkość strumienia ciepła do granicy q = qf + qc + qr :
Metoda elementów skończonych wykorzystywana w programie THERM opiera się na metodzie reszta ważonych, która opiera się na równaniu (6):
W przypadku, gdy w równaniu podstawi się przybliżenie rzeczywistego pola temperatur powstaje funkcja resztkowa ℜ, która wynosi 0 dla dokładnego pola temperatury. Ważona metoda resztkowa nie ma na celu wymuszania funkcji resztkowej w całym obszarze dziedziny na zero. Funkcja resztkowa mnożona jest przez współczynnik ważenia W w celu otrzymania minimalnego błędu przybliżonego rozwiązania:
Wyniki otrzymywane za pomocą obliczeń w programie THERM wykazują dokładność do 1%. Trzeba jednak wziąć pod uwagę, że modelowanie w programie nie odzwierciedla w 100% rzeczywistości. Modelowanie polega na tworzeniu rysunków, a nie wprowadzaniu do programu rzeczywistych komponentów. Dlatego rzeczywiste wyniki symulacji i testów mieszczą się w 10% granicy dokładności [10 ].
Planowanie eksperymentu obliczeniowego do oceny istotności wpływu wybranych czynników
Zgodnie z przyjętym celem badania jako funkcje celu przyjęto temperatury w miejscu mostka termicznego: Y1 ( ϑimg ) – temperaturę na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem z góry stropu, Y2 ( ϑimd ) – temperaturę na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem z dołu stropu.
Warunki modelowania analizowanych detali i warunki brzegowe przyjęto według normy PN-EN ISO 10211 [ 11 ]. Przyjęto gęstość siatki podziałowej równą 1 mm oraz następujące warunki brzegowe:
- dla powierzchni zewnętrznej ściany: temperatura powietrza zewnętrznego te = –22°C, Rse= 0,04 m2·K·W-1,
- dla wewnętrznej powierzchni ściany: temperatura powietrza wewnętrznego ti = 20°C, Rsi= 0,13 m2·K·W-1,
- dla stropu wewnątrz budynku od góry: temperatura powietrza wewnętrznego ti = 20°C, Rsi = 0,17 m2·K·W-1,
- dla stropu wewnątrz budynku od dołu: temperatura powietrza wewnętrznego ti = 20°C, Rsi = 0,10 m2·K·W-1.
Na podstawie analizy rozwiązania konstrukcyjnego węzła połączenia płyty balkonowej ze ścianą i stropem wewnętrznym ( RYS. 11–12 ) zidentyfikowano 12 czynników rzeczywistych, które charakteryzują właściwości cieplne materiałów i wymiary geometryczne wszystkich elementów węzła i mogą wpływać na temperatury ϑimg , ϑimd w charakterystycznych punktach rozpatrywanego węzła. Dodatkowo przyjęto trzy czynniki fikcyjne ( TABELA 1 ).
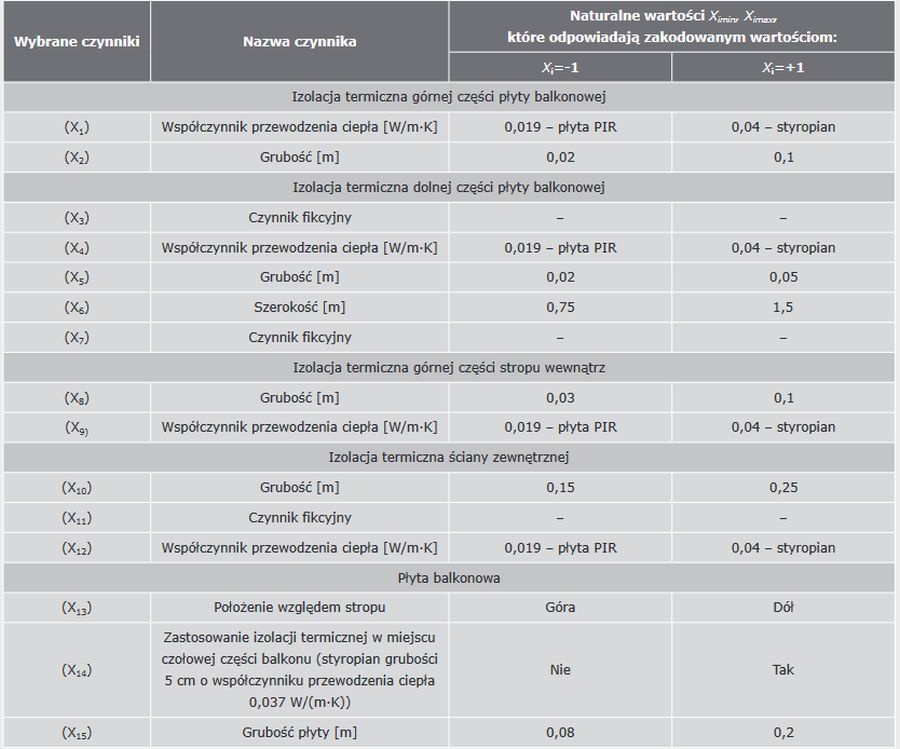
TABELA 1. Zakresy zmienności czynników X1, X2, …X15 wpływających na temperatury ϑimg, ϑimd w charakterystycznych punktach rozpatrywanego węzła
Wyróżniono następujące czynniki:
- w izolacji termicznej górnej części płyty balkonowej: X1 – współczynnik przewodzenia ciepła; X2 – grubość,
- w izolacji termicznej dolnej części płyty balkonowej: X4 – współczynnik przewodzenia ciepła; X5 – grubość; X6 – szerokość,
- w izolacji termicznej górnej części stropu wewnątrz budynku: X8 – grubość; X9 – współczynnik przewodzenia ciepła,
- w izolacji termicznej ściany zewnętrznej: X10 – grubość; X12 – współczynnik przewodzenia ciepła,
- położenie płyty balkonowej względem stropu: X13,
- zastosowanie izolacji termicznej w miejscu czołowym płyty balkonowej: X14,
- grubość płyty balkonowej: X15.
Poziomy czynników zostały dobrane z uwzględnieniem ich przydziału do obszaru adekwatnego, uwzględniając możliwie największy zakres [ 6 ]. Wartości czynników fikcyjnych pominięto.
Po przeanalizowaniu wariantów rozwiązania konstrukcyjnego rozpatrywanego węzła zostały przyjęte zakresy 12 czynników rzeczywistych, które podano w TABELI 1.
W tym badaniu do oceny istotności wpływu wybranych czynników na badane funkcje zastosowano planowanie Placketta-Burmana. Pozwala ono przy realizacji N = 4c doświadczeń, gdzie c - liczba całkowita, ocenić 4c -1 czynników.
Matryce planowania mogą zawierać czynniki rzeczywiste i fikcyjne. Czynniki rzeczywiste w jednym planie mogą występować różne, ale powinny być parametrami sterowalnymi. Należy przyjąć konkretne wartości czynników dla poziomu dolnego i górnego.
Czynniki fikcyjne wprowadzane są w celu obliczenia wartości wariancji doświadczenia. Przy braku pomiarów z powtórnych prób jest to jedyną możliwością wykonania obliczeń wariancji. Zerowe efekty czynników fikcyjnych możliwe są tylko w warunkach, gdy nie ma interakcji pomiędzy czynnikami, a obliczenia są absolutnie dokładne, co w praktyce jest nieosiągalne. Wynika z tego, że 2–4 czynniki fikcyjne pozwalają obliczyć wariancję doświadczenia.
Z uwzględnieniem wybranych 15 czynników należało realizować 16 doświadczeń. Macierz planu opracowano według zasad opisanych w [ 8 ] i przedstawiono w TABELI 2.
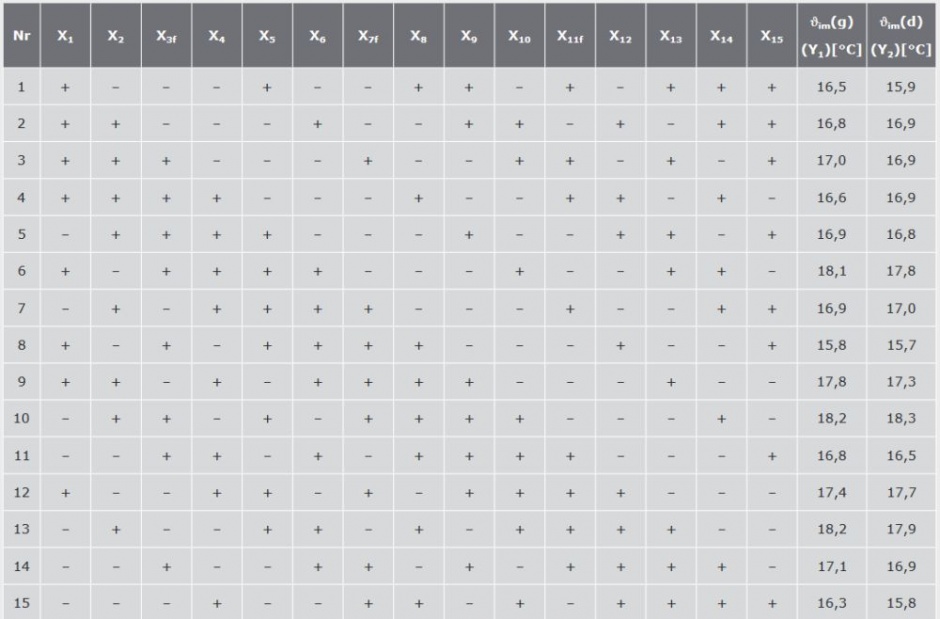
TABELA 2. Macierz planu Placketta-Burmana i wyniki obliczeń temperatur ϑimg, ϑimd w charakterystycznych punktach rozpatrywanego węzła
Do realizacji planu wartości czynników zostały przyjęte na dolnych i górnych poziomach. Znaki (–) oraz (+) w TABELI 2 odpowiadają (-1) oraz (+1) w TABELI 1. Wartości czynników fikcyjnych przy obliczeniach byłe pomijane.
Ocena istotności wpływu badanych czynników na funkcję Y wykonano według [ 12 ] w następującej kolejności:
Obliczono współczynniki istotności αig oraz αid dla poszczególnych badanych czynników według wzoru:
gdzie:
i – numer badanego czynnika,
j – numer doświadczenia,
Xij – wartość i-tej zmiennej w j-tym doświadczeniu,
Yj – wartość funkcji celu w j-tym doświadczeniu,
N – całkowita liczba doświadczeń.
Obliczono wartości wariancji doświadczenia S yg 2 oraz Syd2 według wzoru:
gdzie
l – liczba czynników fikcyjnych,
k – liczba czynników rzeczywistych,
aif – współczynniki istotności dla czynników fikcyjnych.
Obliczono krytyczne wartości współczynników akrg oraz akrd przy założonym poziomie istotności α według wzoru:
gdzie:
t (α;f) – wartość tablicowa współczynnika t-Studenta przy liczbie swobody ƒ = 4l-k-1 i założonym poziomie istotności α.
Obliczone wartości współczynników istotności α jg oraz α jd porównano z krytyczną wartością współczynnika α kr(g) oraz α kr(d) . Jeżeli | αj | ≥ αkr, to wpływ czynnika i-tego na funkcję Y uznawano za istotny przy danym poziomie istotności α.
W taki sposób zostały obliczone i porównane wszystkie wartości współczynników istotności. Wyniki obliczeń podano w TABELI 3.
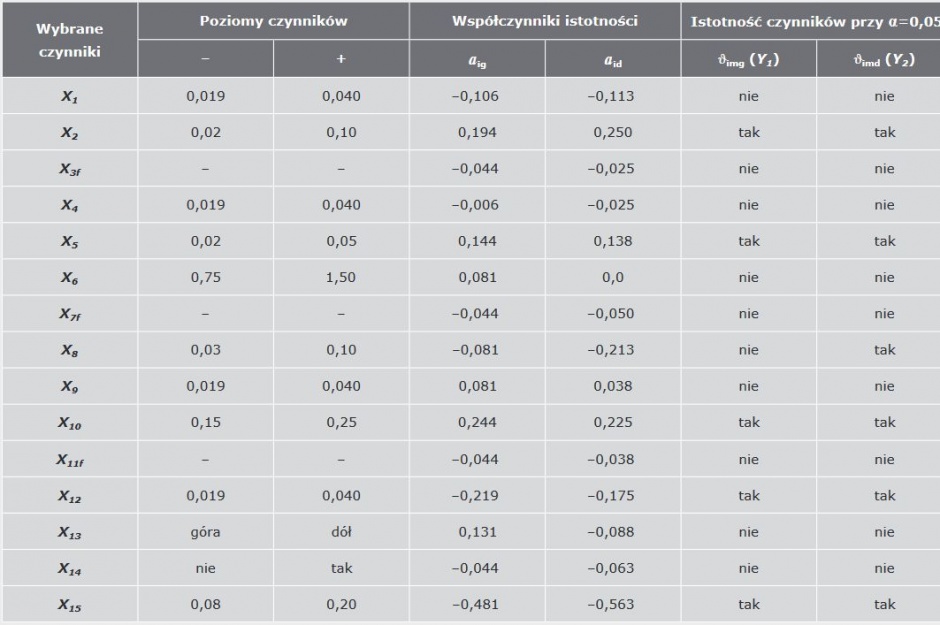
TABELA 3. Wyniki analizy istotności wpływu wybranych czynników na temperaturę ϑimg (Y1) oraz ϑimd (Y2)
Analiza istotności wpływu wybranych czynników na temperaturę powierzchni wewnętrznej przegrody
Przy wykonywaniu analizy istotności wpływu czynników i ustalaniu kryterium t-Studenta wybrano poziom istotności α =0,05. W obliczeniach technicznych to kryterium wykorzystuje się do wyznaczania przedziałów ufności.
Z punktu widzenia praktycznego należało wykonać analizę przy tablicowych wartościach t (0,05;3)= 3,182 [ 12 ].
Wartości wariancji doświadczenia w badaniu okazały się równe: Syg2 = 0,0019; Syd2 = 0,0015.
Wartości krytyczne współczynników istotności odpowiednio wynosiły: αkr(g) = 0,1392 oraz αkr(d) = 0,1237. Wyniki analizy podano w gdzie:
t(α;f) – wartość tablicowa współczynnika t-Studenta przy liczbie swobody ƒ = 4l-k-1 i założonym poziomie istotności α.
Obliczone wartości współczynników istotności α jg oraz α jd porównano z krytyczną wartością współczynnika αkr(g) oraz αkr(d). Jeżeli | αj |≥ αkr, to wpływ czynnika i-tego na funkcję Y uznawano za istotny przy danym poziomie istotności α.
W taki sposób zostały obliczone i porównane wszystkie wartości współczynników istotności. Wyniki obliczeń podano w TABELI 3.
Porównując wartości współczynników istotności | αi |dla czynników rzeczywistych z wartościami krytycznymi αkr(g) oraz αkr(d), wykryto, że przy poziomie istotności α = 0,05 na temperaturę na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem z góry stropu Y1 ( ϑimg ) istotnie wpływa tylko pięć czynników:
- X2 – grubość izolacji termicznej górnej części płyty balkonowej,
- X5 – grubość izolacji termicznej dolnej części płyty balkonowej,
- X10 – grubość izolacji termicznej ściany zewnętrznej,
- X12 – współczynnik przewodzenia ciepła izolacji termicznej ściany zewnętrznej,
- X15 – grubość płyty balkonowej.
Z pięciu istotnych, jako czynniki korzystne, ze wzrostem których temperatura Y1 ( ϑimg ) wzrasta, okazały się trzy:
- X2 – grubość izolacji termicznej górnej części płyty balkonowej,
- X5 – grubość izolacji termicznej dolnej części płyty balkonowej,
- X10 – grubość izolacji termicznej ściany zewnętrznej.
Ze wzrostem czynników X12 – współczynnik przewodzenia ciepła izolacji termicznej ściany zewnętrznej i X15 – grubość płyty balkonowej temperatura Y1 ( ϑimg ) maleje, więc czynniki te zostały uznane za niekorzystne. Natomiast przy tym samym poziomie istotności na temperaturę na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem w dolnej części stropu Y2 ( ϑimd ) istotnie wpływa sześć czynników:
- X2 – grubość izolacji termicznej górnej części płyty balkonowej,
- X5 –grubość izolacji termicznej dolnej części płyty balkonowej,
- X8 – grubość izolacji termicznej górnej części stropu wewnątrz budynku,
- X10 – grubość izolacji termicznej ściany zewnętrznej,
- X12 – współczynnik przewodzenia ciepła izolacji termicznej ściany zewnętrznej,
- X15 – grubość płyty balkonowej.
Z sześciu istotnych, jako czynniki korzystne, ze wzrostem których temperatura Y2 ( ϑimd ) wzrasta, okazały się znów trzy: X2 , X5 i X10 . Ze wzrostem czynników X8 , X12 i X15 temperatura Y2 ( ϑimd ) maleje.
Z analizy istotności wynika, że temperatura Y2 ( ϑimd ) na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem w dolnej części jest krytyczna w rozpatrywanym węźle, ponieważ wpływa na nią więcej czynników i wartości temperatury Y2 ( ϑimd ) są niższe od Y1 ( ϑimg ).
Przy wykonywaniu dalszych badań w celu optymalizacji parametrów rozpatrywanego węzła według kryterium temperaturowego jako funkcję należy przyjąć temperaturę Y2 ( ϑimd ) na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem w jego dolnej części i uwzględnić sześć wyżej podanych istotnych (korzystnych i niekorzystnych) czynników.
Wnioski
Przeprowadzone badanie z zastosowaniem planowania Placketta-Burmana pozwoliło określić istotność wpływu 12 czynników, charakteryzujących właściwości fizyczne i geometryczne węzła połączenia płyty balkonowej ze ścianą, na temperatury ϑimg ( Y1 ) oraz Y2 ( ϑimd ) na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem odpowiednio z góry i z dołu stropu.
Ustalono, że temperatura Y2 ( ϑimd ) na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem z dołu stropu jest krytyczna w rozpatrywanym węźle, ponieważ wpływa na niej najwięcej czynników.
Wykryto, że na temperaturę na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem z dołu stropu Y2 ( ϑimd ) istotnie wpływa sześć czynników: X2 – grubość izolacji termicznej górnej części płyty balkonowej; X5 – grubość izolacji termicznej dolnej części płyty balkonowej; X8 – grubość izolacji termicznej górnej części stropu wewnątrz budynku; X10 – grubość izolacji termicznej ściany zewnętrznej; X12 – współczynnik przewodzenia ciepła izolacji termicznej ściany zewnętrznej; X15 – grubość płyty balkonowej. Wpływ pozostałych dziewięciu rzeczywistych i fikcyjnych czynników na temperaturę Y2 ( ϑimd ) okazał się nieistotny.
Przy wykonywaniu dalszych badań w celu optymalizacji parametrów rozpatrywanego węzła według kryterium temperaturowego jako funkcję należy przyjmować temperaturę Y2 ( ϑimd ) na wewnętrznej powierzchni ściany zewnętrznej na styku ze stropem w jego dolnej części i uwzględniać sześć wyżej podanych istotnych czynników.
Literatura
1. M. Rokiel, „ABC tarasów i balkonów”, Grupa Medium, Warszawa 2019.
2. Strona internetowa: https://www.schoeck.com/pl/home
3. Strona internetowa: https://extrea.pl/thermotec-laczniki-balkonowe
4. K. Pawłowski, „Balkony – projektowanie numeryczne złączy z uwzględnieniem wymagań cieplno-wilgotnościowych od 1 stycznia 2021 roku”, „IZOLACJE” 4/2020.
5. M. Grudzińska, „Cieplno-wilgotnościowa ocena mostków cieplnych”, „IZOLACJE”.
6. M. Korzyński, „Metodyka eksperymentu”, WNT, Warszawa 2013.
7. A. Łapko, „Projektowanie konstrukcji żelbetowych”, Arkady, Warszawa 2001.
8. THERM 7.6: https://windows.lbl.gov/software-release-therm-7601
9. THERM 2.0: Program Description, A PC Program for Analyzing the Two-Dimensional Heat Transfer Through Building Products, Elizabeth Finlayson, Robin Mitchell, and Dariush Arasteh, Windows and Daylighting Group, Building Technologies Department Environmental Energy Technologies Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720.
10. M. Sealander, AIA, Maine Licensed Architect, Using LBNL Therm for Energy Analysis, Sealanders Architects.
11. PN-EN ISO 10211-1, „Mostki cieplne w budynkach. Obliczanie strumieni cieplnych i temperatury powierzchni. Część 1: Metody ogólne”.
12. J. Gutenbaum, „Modelowanie matematyczne systemów”, Akademicka Oficyna Wydawnicza Exit, Warszawa 2003.
13. PN-EN ISO 13788:2013-05, „Cieplno-wilgotnościowe właściwości komponentów budowlanych i elementów budynku – Temperatura powierzchni wewnętrznej konieczna do uniknięcia krytycznej wilgotności powierzchni i kondensacji międzywarstwowej – Metody obliczania”.
14. Conrad 5 & Viewer 5 Technical and Programming Documentation https://windows.lbl.gov/sites/all/files/Downloads/conrad-and-viewer-06-20-06.pdf
15. THERM 5.2/WINDOW 5.2 NFRC Simulation Manual Robin Mitchell, Christian Kohler, and Dariush Arasteh, Windows and Daylighting Group, Building Technologies Department Environmental Energy Technologies Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720.
16. P.L. Baehmann, S.L. Wittchen, M.S. Shephard, K.R. Grice, M.A. Yerry, „Robust, Geometrically Based, Automatic Two-Dimensional Mesh Generation”, „International Journal for Numerical Methods in Engineering” 24/1987, pp. 1043–1078.
17. O.C. Zienkiewicz, J.Z. Zhu, „The Superconvergent Patch Recovery and A Posteriori Error Estimates. Part 1: The Recovery Technique.” International Journal for Numerical Methods in Engineering”, Vol 33, 1992, pp. 1331–1364.