Obliczanie odporności ogniowej konstrukcji stalowych na podstawie euronomogramów

Tradycyjna metoda projektowania konstrukcji stalowych pod kątem bezpieczeństwa pożarowego polega na doborze środków ochrony przeciwpożarowej, w szczególności odpowiednich paramentów izolacji termicznej osłaniającej stalowy ustrój nośny obiektu przed działaniem ognia i chroniącej przed zbyt gwałtownym nagrzewaniem. Ten sposób zabezpieczenia ogniochronnego konstrukcji stalowych omówiono m.in. w artykułach opublikowanych na łamach „IZOLACJI” [1, 2]. Metoda ta ogranicza się do prostego wyboru środków ognioizolujących (z wykorzystaniem jedynie dostępnych materiałów). Zwykle stosuje się ją w odniesieniu do stosunkowo prostych budynków i w wielu przypadkach może być zbyt zachowawcza.

Aby zapewnić wymaganą ognioodporność konstrukcji stalowej metodą tradycyjną, należy zastosować kosztochłonną, bierną ochronę przeciwpożarową. W takim projektowaniu nie przeprowadza się żadnej dodatkowej analizy obliczeniowej oceniającej zachowanie się konstrukcji stalowej w trakcie pożaru. Nie uwzględnia się np. swobody odkształceń termicznych i stopnia „skrępowania” konstrukcji stalowej, powstałych wskutek działania sił wewnętrznych wywołanych wymuszonymi lub ograniczonymi wydłużeniami. Tymczasem te dodatkowe siły wewnętrzne mogą być przyczyną wyczerpania nośności konstrukcji, co może prowadzić do awarii lub katastrofy obiektu (fot. 1–4) [3].

Wiarygodną ocenę ognioodporności konstrukcji nośnej obiektu można uzyskać na podstawie odrębnej analizy termiczno-statyczno-wytrzymałościowej (według metody opartej na właściwościach). Ogólne zasady ustalania oddziaływań oraz projektowania w warunkach pożaru podano w normie PN-EN 1991-1-2:2006 [4].

Proste metody obliczeniowe konstrukcji stalowych w warunkach pożaru według normy PN-EN 1993-1-2:2007 [5] to metoda nośności i metoda temperatury krytycznej. W metodzie nośności stosuje się modele mechaniczne i przeprowadza weryfikację nośności konstrukcji. Obie metody projektowania (przedstawione w pracy „Pożarowe uszkodzenie i naprawa hali” [3]) służą do analizy bezpieczeństwa pożarowego typowych stalowych elementów konstrukcyjnych, np. belek i słupów. Natomiast zaawansowane modele obliczeniowe mogą być stosowane do wszystkich rodzajów konstrukcji i umożliwiają realistyczną analizę termiczno-statyczno-wytrzymałościową. Wyniki tej analizy zazwyczaj są uzyskiwane w postaci odkształceń konstrukcji podczas całego okresu pożaru. Zaawansowane modele obliczeniowe przeprowadza się metodą elementów skończonych (MES) za pomocą programów komputerowych.

Analiza termiczna elementów stalowych bez izolacji ogniochronnej oraz z izolacją ogniochronną

Celem analizy termicznej jest określenie zależności między temperaturą stalowego elementu θ_a,t a czasem t osiągnięcia tej temperatury (zarówno w przypadku elementów nieosłoniętych izolacją ogniochronną, jak i osłoniętych). Dzięki wyznaczeniu temperatury w elemencie stalowym w rozważanym czasie t trwania pożaru można ocenić stopień wytężenia w pożarze, a także wyznaczyć odkształcenia termiczne.

Parametr A_m/V [m^–1] nazywa się wskaźnikiem ekspozycji przekroju (lub wskaźnikiem masywności przekroju). Jest on miarą szybkości nagrzewania się stalowego elementu nieosłoniętego narażonego na oddziaływanie wysokiej temperatury w warunkach pożaru. Ponadto w ocenie ilości ciepła przejmowanego przez taki element stalowy uwzględnia się współczynnik poprawkowy ksh związany z efektem zacienienia. Współczynnik k_sh jest ilorazem umownego przekroju skrzynkowego opisanego na przekroju rzeczywistym [Am/V]b i wskaźnika ekspozycji A_m/V. Sposób ustalania wskaźników przekrojów kształtowników stalowych A_m/V [m^–1] oraz [A_m/V]_sh podano w normie PN-EN 1993­‑1­‑2:2007 [5], a także w artykułach opublikowanych na łamach „IZOLACJI” [1, 2].

W normie PN-EN 1993-1-2:2007 [5] podano metodę obliczeniową oceny nagrzewania się stalowych elementów nieizolowanych ogniochronnie w przypadku równoważnego, równomiernego rozkładu temperatury w przekroju. Przyrost temperatury Δθ_a,t w przedziale czasu Δt w stalowym elemencie nieosłoniętym zapisany jest w postaci przyrostowej. Aby określić odpowiednik w wartościach całkowitych, należy przyjąć model pożaru i scałkowania po czasie (np. zastosować jawny algorytm całkowania po czasie). W tabeli 1 [6] podano wartości temperatury θ_a,t po czasie t w przekrojach stalowych elementów konstrukcyjnych bez izolacji ogniochronnej, przy różnych wartościach współczynnika ekspozycji A_m*/V = k_sh (Am/V), obliczonych w odniesieniu do standardowej krzywej ekspozycji pożarowej.

Aby wydłużyć czas dochodzenia w warunkach pożaru do temperatury krytycznej konstrukcji stalowej, czyli zwiększyć odporność ogniową, stosuje się m.in. bierną ochronę przeciwpożarową (osłony ognioizolacyjne). W przypadku elementu osłoniętego wskaźnik masywności przekroju przyjmuje się jako parametr A_p/V [m^–1]. Zasady ustalania wskaźników przekrojów kształtowników stalowych A_p/V podano w normie PN-EN 1993-1-2:2007 [5], a także we wspomnianych artykułach opublikowanych w „IZOLACJACH” [1, 2].

W normie PN-EN 1993-1-2:2007 [5] podano również metodę obliczeniową oceny nagrzewania się stalowych elementów izolowanych materiałami biernej ochrony przeciwpożarowej. W takich przypadkach wzrost temperatury zależy od wskaźnika masywności przekroju stalowego elementu izolowanego A_p/V [m^–1], grubości warstwy izolacji ogniochronnej d_p [m] oraz jej przewodności cieplnej λp [W/(m·K)], które wyraża wskaźnik izolacyjności przekroju kp [W/(m³·K)] określony wzorem:

Właściwości fizyczne (m.in. przewodność cieplną λp) podstawowych materiałów stosowanych do wykonania izolacji ogniochronnych stalowych elementów konstrukcyjnych omówiono m.in. w pracach „Czynne i bierne zabezpieczenia ogniochronne konstrukcji stalowych” [1] oraz „Design of Steel Structures Subjected to Fire. Background and Design Guide to Eurocode 3” [6]. W tabeli 2 [6] podano wartości temperatury θ_a,t po czasie t stalowego elementu osłoniętego izolacją ogniochronną, przy założeniu standardowego modelu pożaru, w zależności od wskaźnika izolacyjności przekroju k_p.

Proste metody projektowania oraz określania wydłużenia konstrukcji stalowych

Zachowanie stalowego elementu konstrukcyjnego podczas pożaru standardowego omówiono w kilku pracach naukowo-technicznych [1, 2, 6–8].

Gdy w warunkach pożaru temperatura gazu θ_g wzrasta, zwiększa się temperatura elementu stalowego θ_a,t, a jego nośność R_fi,d,t maleje. Konstrukcje stalowe należy projektować w sposób, który pozwoli zapewnić nośność R_fi,d,t (lub ograniczyć odkształcenia) przez pewien czas t_fi,d,req, w którym są one narażone na działanie wysokiej temperatury występującej w trakcie pożaru. Czas t_fi,d,req charakteryzuje klasę odporności pożarowej budynku.

W normie PN-EN 1993-1-2:2007 [5] zaproponowano proste modele obliczania nośności belek i słupów stalowych w warunkach pożaru, tj. metodę temperatury krytycznej oraz metodę nośności. Można je stosować w ocenie nośności elementów stalowych niezabezpieczonych i zabezpieczonych ogniochronnie oraz chronionych ekranami cieplnymi. W tych uproszczonych modelach obliczeniowych nie uwzględnia się sił wewnętrznych spowodowanych wymuszonymi lub ograniczonymi wydłużeniami ani deformacjami elementów konstrukcji stalowej.

Temperatura krytyczna stalowego elementu nośnego θ_a,cr (przy danym poziomie jego obciążenia) to temperatura, w której element ulega zniszczeniu. Ognioodporność elementu stalowego jest zapewniona po czasie t, jeżeli temperatura stali θa,t nie przekracza jej temperatury krytycznej θ_a,cr:

θ_a,t ≤ θ_a,cr (2)

W tym przypadku, na podstawie analizy termicznej, należy wyznaczyć temperaturę elementu stalowego θ_a,t po czasie t oraz jego temperaturę krytyczną θ_a,cr.

Zgodnie z normą PN-EN 1993-1-2:2007 [5] w ocenie bezpieczeństwa elementów stalowych w warunkach pożaru można stosować metodę nośności. W analizie prostych modeli obliczeniowych ocenę odporności ogniowej konstrukcji stalowej metodą nośności sprawdza się ze wzoru:

E_fi,d≤ R_fi,d,t (3)

gdzie:

E_fi,d – obliczeniowy efekt oddziaływań (M_fi,Ed, N_fi,Ed, V_fi,Ed) w sytuacji pożarowej wyznaczony zgodnie z normą PN-EN 1991-1-2:2006 [4],

R_fi,d,t – obliczeniowa nośność elementu stalowego (M_fi,Rd, N_fi,Rd, V_fi,Rd) części lub całości konstrukcji po czasie t, obliczona według normy PN-EN 1993-1-2:2007 [5].

Obliczeniowe nośności elementów stalowych w warunkach pożaru R_fi,d,t określa się na podstawie modyfikacji odpowiednich ich nośności określanych w normalnej temperaturze według postanowień normy PN-EN 1993-1-1:2006 [9]. Metodę nośności można stosować w ocenie wytrzymałości w warunkach pożaru elementów rozciąganych, ściskanych lub/i zginanych. Przykłady obliczeń nośności konstrukcji stalowych w warunkach pożaru tą metodą przedstawiono m.in. w pracach „Projektowanie stalowych elementów rozciąganych, ściskanych i zginanych z uwagi na warunki pożarowe według PN-EN 1993-1-2” [7] oraz „Odporność ogniowa. Nośność konstrukcji w warunkach pożaru” [8].

Jeśli analizowany stalowy element konstrukcyjny ma pełną swobodę odkształceń termicznych (wydłużania oraz obrotów w węzłach i połączeniach), można przyjąć, że w wyniku rosnącej temperatury θ_a,t nie powstają żadne dodatkowe siły wewnętrzne. Jeśli natomiast ten warunek nie jest spełniony (występują odkształcenia termiczne oraz „skrępowanie” konstrukcji), w analizie termiczno-statyczno-wytrzymałościowej należy uwzględnić m.in. wydłużenia termiczne.

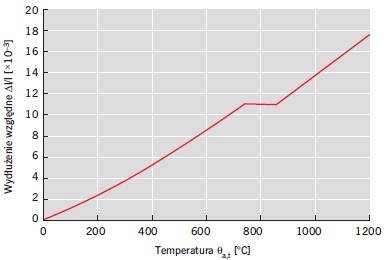
Zgodnie z normą PN-EN 1993-1-2:2007 [5] względne wydłużenia termiczne stali węglowej Δl/l można wyznaczyć według następujących zależności:

• 20°C ≤ θ_a,t < 750°C
  Δl/l = 1,2 · 10^–5 θ_a,t + 0,4 · 10^–8 θ²_a,t – 2,416 · 10^–4 (4)
• 750°C ≤ θ_a,t ≤  860°C
  Δl/l = 11 · 10^–2 (5)
• 860°C ≤ θ_a,t < 1200°C
  Δl/l = 2 · 10^–5 θ_a,t – 6,2 · 10^–3 (6)

gdzie:

l – długość w temp. 20°C,

Δl – wydłużenie spowodowane temperaturą,

θ_a,t – temperatura stali [°C].

Względne wydłużenie stali węglowej Δl/l w funkcji temperatury θ_a,t pokazano na rys. 1 [5].

W ramach badań naukowych prowadzonych przez Europejską Konwencję Konstrukcji Stalowych (ECSC) opracowano tzw. euronomogramy [10–15] ułatwiające obliczenia dotyczące konstrukcji stalowych w warunkach pożaru według metody nośności i metody temperatury krytycznej. Zaproponowane procedury obliczeniowe są szczególnie przydatne w przypadku analizy nośności z warunku utraty stateczności ogólnej elementów stalowych (nośności na wyboczenie oraz nośności na zwichrzenie).

Ocena metodą temperatury krytycznej na podstawie euronomogramów

Podstawą oceny bezpieczeństwa pożarowego metodą temperatury krytycznej jest wyznaczenie temperatury θ_a,t elementu stalowego po upływie wymaganego okresu ognioodporności t_fi,d,req i porównanie jej z temperaturą krytyczną θ_a,cr, przy której wystąpiłoby wyczerpanie nośności, tj. sprawdzenie warunku (2). Ten prosty model obliczeniowy metody temperatury krytycznej można stosować tylko wtedy, gdy nie trzeba uwzględniać ani kryteriów stateczności w analizie wytrzymałościowej (w przypadku prętów rozciąganych, zginanych zabezpieczonych przed zwichrzeniem oraz ściskanych, które nie ulegają wyboczeniu), ani warunków odkształcenia elementu stalowego.

Temperatura krytyczna θ_cr stalowego elementu o przekroju klasy 1, 2 lub 3 wynosi 500–800°C. Oblicza się ją (przy założeniu równomiernego rozkładu temperatury) ze wzoru:

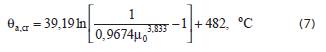
w którym wskaźnik wykorzystania nośności elementu µ₀ wyznacza się z zależności:

gdzie:

E_fi,d – efekt oddziaływań na konstrukcję, wyznaczony zgodnie z regułami wyjątkowej obliczeniowej sytuacji pożarowej według normy PN-EN 1991-1-2:2006 [4],

R_fi,d,0 – nośność obliczeniowa elementu stalowego w obliczeniowej sytuacji pożarowej w czasie t = 0.

W przypadku kształtowników o przekrojach klasy 4 należy stosować zachowawczą temperaturę krytyczną θ_a,cr = 350°C.

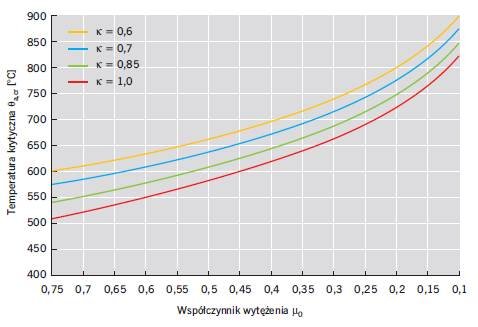
Na rys. 2 [13] pokazano nomogramy temperatury krytycznej elementów stalowych θ_a,cr w funkcji wskaźnika wykorzystania nośności µ₀. Służą one do obliczania odporności ogniowej stalowych prętów rozciąganych i belek z uwzględnieniem współczynnika przystosowania (adaptacji).

W normie PN-EN 1993-1-2:2007 [5] podano uproszczone zasady oceny nośności na zginanie stalowych elementów o przekrojach klasy 1, 2 lub 3, o nierównomiernym rozkładzie temperatury w przekroju oraz na ich długości. W tym podejściu obliczeniową nośność na zginanie można obliczyć ze wzoru:

gdzie:

M_fi,θ,Rd – obliczeniowa nośność przy zginaniu z równomierną temperaturą w przekroju θ_a,t w czasie t trwania pożaru, według normy PN-EN 1993-1-2:2007 [5],

K₁, K₂ – współczynnik przystosowania uwzględniający nierównomierny rozkład temperatury w przekroju (tabela 3 [5]) oraz na długości (tabela 4 [5]).

Na rys. 2 [13] pokazano nomogramy temperatury krytycznej stalowych elementów zginanych zabezpieczonych przed zwichrzeniem oraz prętów rozciąganych w funkcji współczynników przystosowania K = K₁ · K₂ = 0,60, 0,70, 0,85, i 1,00 oraz zmodyfikowanego współczynnika stopnia ich wytężenia µ₀, obliczonego ze wzoru:

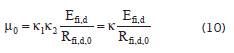
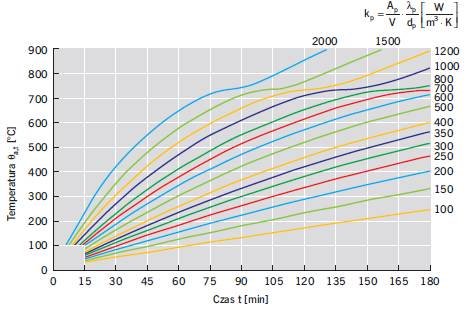
Temperaturę θ_a,t po czasie t stalowych elementów nieosłoniętych izolacją ogniochronną oraz osłoniętych izolacją ogniochronną można wyznaczyć za pomocą danych zawartych w tabelach 1–2 lub euronomogramów, które pokazano na rys. 3–4 [10–11]. Potrzebne do określenia temperatury θ_a,t wartości wskaźników przekrojów walcowanych na gorąco kształtowników stalowych (odpowiednio [A_m/V]_sh oraz A_p/V) można określić za pomocą tablic podanych na stronach producentów stali [10–11, 16].

Temperatura krytyczna elementu stalowego θ_a,cr zmniejsza się wraz ze wzrostem wskaźnika wykorzystania nośności µ₀. W odniesieniu do danego czasu trwania pożaru t (jeśli przyjąć, że θ_a,t = θ_a,cr) na podstawie nomogramów na rys. 2 [13] można wyznaczyć maksymalną wartość poziomu wykorzystania nośności µ₀ elementu stalowego.

Ocena metodą nośności na podstawie euronomogramów

Zgodnie z normą PN-EN 1993-1-2:2007 [5] metoda nośności oceny bezpieczeństwa pożarowego polega na obliczeniu wytrzymałości elementu stalowego w podwyższonej temperaturze R_fi,d,t po upływie wymaganego czasu ognioodporności t i porównaniu jej z efektem oddziaływań na konstrukcję w warunkach pożaru E_fi,d. Ocenę odporności ogniowej konstrukcji stalowej metodą nośności sprawdza się według wzoru (3).Zastosowana w normie PN-EN 1993-1-2:2007 [5] metoda nośności jest kompatybilna z zasadami obliczania nośności konstrukcji stalowych w warunkach normalnej temperatury według normy PN­‑EN 1993-1-1:2006 [9]. Umożliwia ocenę wytrzymałości elementów rozciąganych, ściskanych (z warunku wyboczenia) lub/i zginanych (z warunku zwichrzenia).

Procedury określenia nośności prętów z warunku utraty stateczności ogólnej elementów stalowych w czasie pożaru R_b,fi,d,t (ściskanych N R_b,fi,d,t lub zginanych M_b,fi,d,t) według normy PN-EN 1993­‑1­‑2:2007 [5] różnią się w niektórych aspektach od algorytmów stosowanych do obliczania nośności elementów R_b,d w normalnej temperaturze według normy PN-EN 1993-1-1:2006 [9]. Dotyczy to m.in. przyjmowania wielokrotnych krzywych niestateczności ogólnej, a wynika z konieczności uwzględnienia zmian granicy plastyczności f_y,θ oraz modułu sprężystości podłużnej E_θ w podwyższonych temperaturach, które bezpośrednio decydują o nośności z warunku utraty stateczności ogólnej.

W procedurze określenia nośności na wyboczenie lub zwichrzenie prętów stalowych w warunkach pożaru można wyróżnić cztery kroki obliczeniowe:

• wyznaczenie smukłości względnej niestateczności ogólnej w warunkach pożaru (wyboczenia λ_θ lub zwichrzenia λ_LT,θ),
• obliczenie parametru imperfekcji α jako funkcji granicy plastyczności stali k_y,θ,
• określenie współczynnika niestateczności ogólnej (wyboczenia χ_fi lub zwichrzenia χ_LT,fi),
• obliczenie nośności elementu stalowego w trakcie pożaru na wyboczenie N_b,fi,t,Rd lub na zwichrzenie M_b,fi,t,Rd.

Smukłości względne wyboczenia λ_θ lub zwichrzenia λ_LT,θ w warunkach pożaru zależą od temperatury, ponieważ są funkcją współczynników redukcyjnych granicy proporcjonalności, granicy plastyczności k_y,θ oraz modułu sprężystości podłużnej stali k_E,θ. Z tego powodu temperaturę krytyczną odpowiadającą danemu poziomowi efektu oddziaływań N_fi,Ed lub M_fi,Ed oblicza się iteracyjnie (powtarza się wymienione cztery kroki obliczeniowe). Na ogół do osiągnięcia zadowalającej zbieżności obliczeń wystarcza druga lub trzecia iteracja (proces iteracyjny jest szybkozbieżny). Iterację powtarza się do uzyskania tej samej wartości współczynnika redukcyjnego granicy plastyczności stali k_y,θ w dwóch kolejnych iteracjach. Wówczas przyjmuje się, że temperatura θa wyznaczona w ostatniej iteracji jest temperaturą krytyczną θ_a,cr.

Przedstawiony iteracyjny sposób oceny nośności prętów stalowych z warunku utraty stateczności ogólnej (wyboczenia i ­zwichrzenia) według postanowień normy PN-EN 1993­‑1­‑2 [5] można usprawnić dzięki zastosowaniu nomogramów ze strony internetowej jednego z producentów stali [12, 14, 15].

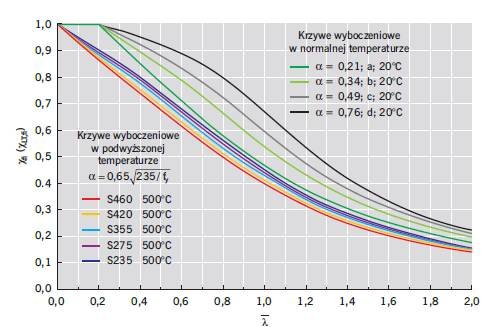
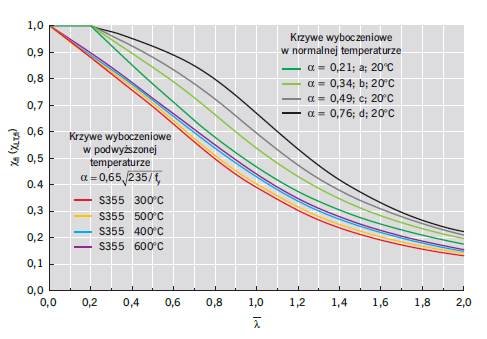
Krzywe niestateczności ogólnej χ_fi i χ_LT,fi w warunkach pożaru zależą od temperatury stali θ_a,t, jej granicy plastyczności (są funkcją współczynnika redukcyjnego k_y,θ) i modułu sprężystości podłużnej (są funkcją współczynnika redukcyjnego k_E,θ) oraz parametru imperfekcji α, co pokazano na rys. 5–6.

Na rys. 5 pokazano krzywe niestateczności ogólnej χ_fi (wyboczenia) oraz χ_fi (zwichrzenia) elementów ze stali S235, S275, S355, S420 i S460 w temp. 500°C w funkcji smukłości względnej λ. Rysunek ten ilustruje wpływ wartości granicy plastyczności na wartość współczynnika niestateczności ogólnej. Z kolei na rys. 6 pokazano krzywe niestateczności ogólnej χ_fi(wyboczenia) oraz χ_fi (zwichrzenia) elementów ze stali S355 w temp. 300°C, 400°C, 500°C i 600°C w funkcji smukłości względnej λ. Rysunek przedstawia wpływ wzrostu temperatury na redukcję krzywych niestateczności ogólnej. Z analizy wykresów wynika, że krzywe wyboczeniowe w warunkach pożaru są zredukowane w stosunku do krzywych niestateczności w temperaturze normalnej. Ponadto wzrost temperatury stali powoduje wzrost redukcji wartości współczynnika wyboczeniowego.

Współczynniki niestateczności ogólnej (wyboczenia χ_fi i zwichrzenia χ_LT,fi) elementów ze stali S235, S275, S355, S420 i S460 w podwyższonych temperaturach θ_a,t można wyznaczyć na podstawie tablic podanych na stronie internetowej producenta stali [12].

Uproszenie iteracyjnego sposobu oceny nośności słupów w warunkach pożaru zaproponowano w SD0010a-EN-EU [14] (na podstawie wyników projektu badawczego Europejskiej Konwencji Konstrukcji Stalowych (ECSC) [15]). Podano tabele zależności między granicznymi nieprężeniami ściskającymi f’_y,θ,λ smukłością pręta λ i temperaturą stali θ_a,t. Dane te służą do obliczania odporności ogniowej słupów stalowych nieizolowanych obciążonych osiowo i równomiernie nagrzanych. Obliczeniową nośność na wyboczenie N_b,fi,t,Rd elementów o przekrojach klasy 1, 2 lub 3 oraz o równomiernym rozkładzie temperatury stali θ_a,t określa się ze wzoru:

gdzie:

χ_fi – współczynnik wyboczenia giętego w sytuacji pożarowej,

A – pole przekroju elementu ściskanego,

k_y,θ – współczynnik redukcyjny granicy plastyczności stali,

f_y – granica plastyczności stali,

f’_y,θ,λ – graniczne naprężenia ściskające w warunkach pożaru, opisane zależnością:

Wartości granicznych naprężeń ściskających w warunkach pożaru f’_y,θ,λ stali S235, S275, S355 i S460 podano w „Limiting compressive stresses for the design fire resistance of steel columns” [14]. W tabeli 5 przedstawiono przykładowe graniczne naprężenia ściskające f’_y,θ,λ dla stali S235 [14]. Zależą one od analizowanej temperatury stali θ_a,t i smukłości względnej λ w temperaturze normalnej (20°C). Smukłość względną λ w temp. 20°C należy przyjmować w sposób podany w normie PN-EN 1993-1-1:2006 [9]. Długości wyboczeniowe słupów le określa się jak przy projektowaniu elementów w normalnej temperaturze, z wyjątkiem słupów ciągłych w stężonych układach ramowych. Wówczas należy przyjąć długość wyboczeniową:

• l_e = 0,5L – w odniesieniu do słupów kondygnacji pośrednich,
• l_e = 0,7L – w odniesieniu do słupów kondygnacji najwyższej,

gdzie:

L – długość teoretyczna słupa rozpatrywanej kondygnacji.

Na podstawie smukłości względnej λ oraz wartości temperatury założonej w warunkach pożaru θ_a,t można wyznaczyć graniczne naprężenia ściskające f’_y,θ,λ (na podstawie tablic [14]), a następnie ze wzoru (11) określić obliczeniową nośność pręta stalowego na wyboczenie N_b,fi,t,Rd.

Podsumowanie

W celu spełnienia wymagań ognioodporności konstrukcji stalowych najczęściej stosuje się tradycyjną metodę projektowania. Ogranicza się ona do prostego wyboru kosztownych zabezpieczeń ognioizolujących. Nie przeprowadza się wówczas żadnych obliczeń oceniających zachowanie się konstrukcji podczas pożaru. Nie uwzględnia się np. swobody odkształceń termicznych i stopnia „skrępowania” konstrukcji stalowej, które mogą być przyczyną destrukcji, awarii lub katastrofy obiektu.

Obiektywną ocenę ognioodporności można uzyskać na podstawie analizy termiczno-statyczno-wytrzymałościowej konstrukcji, według metody opartej na właściwościach. Metoda ta daje możliwość wyboru rozwiązań technicznych i uwzględnia intensywność oddziaływania pożaru. Na podstawie uzyskanych pól temperatury w elementach i kombinacji oddziaływań można ocenić zachowanie konstrukcji podczas pożaru.

Zaproponowane w normie PN-EN 1993-1-2:2007 [5] relatywnie proste modele obliczeniowe metody nośności i metody temperatury krytycznej umożliwiają weryfikację nośności ogniowej konstrukcji. Ich procedury obliczeniowe można znacznie uprościć dzięki wykorzystaniu euronomogramów [10–15] dotyczących analizy elementu (według modelu 1D). Wówczas w obliczeniach pomija się siły wewnętrzne wywołane wymuszonymi lub ograniczonymi wydłużeniami, a także deformacjami. Taką analizę można stosować w ocenie nośności w warunkach pożaru „wyizolowanych” elementów stalowych rozciąganych, ściskanych (na wyboczenie) lub/i zginanych (na zwichrzenie).

Termiczno-statyczno-wytrzymałościowa analiza całej konstrukcji (według modelu 3D) lub jej podzespołów (według modelu 2D) bierze pod uwagę łącznie co najmniej kilka elementów, tak aby bezpośrednio uwzględnić wpływ interakcji między nimi. Umożliwia znacznie lepsze zrozumienie ogólnego zachowania konstrukcji w warunkach pożaru. Wymaga jednak stosowania zaawansowanych modeli obliczeniowych przeprowadzanych metodą elementów skończonych (MES) za pomocą programów komputerowych.

Literatura

1. A. Biegus, „Czynne i bierne zabezpieczenia ogniochronne konstrukcji stalowych”, „Izolacje”, nr 3/2013, s. 38–48.
2. A. Biegus, „Projektowanie konstrukcji stalowych z uwagi na warunki pożarowe według eurokodów”, „Izolacje”, nr 2/2013, s. 20–28.
3. A. Biegus, „Pożarowe uszkodzenie i naprawa hali”, [w:] materiały XXVI Konferencji Naukowo-Technicznej „Awarie budowlane”, Międzyzdroje, 21–24 maja 2013 [publikacja w przygotowaniu do druku].
4. PN-EN 1991-1-2:2006, „Eurokod 1: Oddziaływania na konstrukcje. Część 1–2: Oddziaływania ogólne. Oddziaływania na konstrukcje w warunkach pożaru”.
5. PN-EN 1993-1-2:2007, „Eurokod 3: Projektowanie konstrukcji stalowych. Część 1–2: Reguły ogólne. Obliczanie konstrukcji z uwagi na warunki pożarowe”.
6. J.M. Franssen, R. Zaharia, „Design of Steel Structures Subjected to Fire. Background and Design Guide to Eurocode 3”, Les Editions Universite de Liege, Liege 2005.
7. M. Giżejowski, P. Król, „Projektowanie stalowych elementów rozciąganych, ściskanych i zginanych z uwagi na warunku pożarowe według PN-EN 1993-1-2”, „Inżynieria i Budownictwo”, nr 9/2008, s. 485–495.
8. M. Maślak, „Budownictwo ogólne”, t. 5, cz. 10: „Odporność ogniowa. Nośność konstrukcji w warunkach pożaru”, Wydawnictwo Arkady, Warszawa 2010.
9. PN-EN 1993-1-1:2006, „Eurokod 3: Projektowanie konstrukcji stalowych. Część 1–1: Reguły ogólne i reguły dla budynków”.
10. SD004a-EN-EU, „Nomogram for unprotected members”, strona internetowa: www.steel-access.com
11. SD005a-EN-EU, „Nomogram for protected members”, strona internetowa: www.steel-access.com
12. SD008a-EN-EU, „Buckling factors at elevated temperature”, strona internetowa: www.steel-access.com
13. SD009a-EN-EU, „Critical temperatures for the design fire resistance of steel beams and members in tension”, strona internetowa: www.steel-access.com
14. SD0010a-EN-EU, „Limiting compressive stresses for the design fire resistance of steel columns”, strona internetowa: www.steel-access.com
15. ECSC project: „Buckling curves of hot rolled H sections submitted to fire”;C No. 7210-SA/316/515/618/931.
16. Strona internetowa: www.arcelormittal.com

Chcesz być na bieżąco? Zapisz się do naszego newslettera!